K11a320

K11a319

K11a321

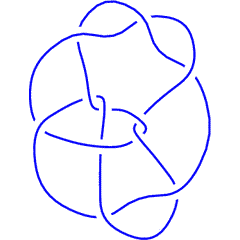(Knotscape image)	See the full Hoste-Thistlethwaite Table of 11 Crossing Knots. Visit K11a320 at Knotilus!

Knot presentations

Planar diagram presentation	X6271 X12,4,13,3 X16,6,17,5 X22,8,1,7 X18,10,19,9 X4,12,5,11 X20,14,21,13 X2,16,3,15 X10,18,11,17 X8,20,9,19 X14,22,15,21
Gauss code	1, -8, 2, -6, 3, -1, 4, -10, 5, -9, 6, -2, 7, -11, 8, -3, 9, -5, 10, -7, 11, -4
Dowker-Thistlethwaite code	6 12 16 22 18 4 20 2 10 8 14

A Braid Representative
A Morse Link Presentation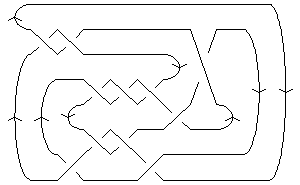

Three dimensional invariants

Symmetry type Chiral Unknotting number $\{2,3\}$ 3-genus 2 Bridge index 3 Super bridge index Missing Nakanishi index Missing Maximal Thurston-Bennequin number Data:K11a320/ThurstonBennequinNumber Hyperbolic Volume 15.7364 A-Polynomial See Data:K11a320/A-polynomial

[edit Notes for K11a320's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus Missing Topological 4 genus Missing Concordance genus $2$ Rasmussen s-Invariant -4

[edit Notes for K11a320's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$9t^{2}-27t+37-27t^{-1}+9t^{-2}$
Conway polynomial	$9z^{4}+9z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 109, 4 }
Jones polynomial	$-q^{13}+3q^{12}-7q^{11}+11q^{10}-15q^{9}+17q^{8}-17q^{7}+16q^{6}-11q^{5}+7q^{4}-3q^{3}+q^{2}$
HOMFLY-PT polynomial (db, data sources)	$z^{4}a^{-4}+3z^{4}a^{-6}+4z^{4}a^{-8}+z^{4}a^{-10}+z^{2}a^{-4}+4z^{2}a^{-6}+7z^{2}a^{-8}-2z^{2}a^{-10}-z^{2}a^{-12}+a^{-6}+3a^{-8}-3a^{-10}$
Kauffman polynomial (db, data sources)	$2z^{10}a^{-10}+2z^{10}a^{-12}+6z^{9}a^{-9}+10z^{9}a^{-11}+4z^{9}a^{-13}+9z^{8}a^{-8}+8z^{8}a^{-10}+2z^{8}a^{-12}+3z^{8}a^{-14}+8z^{7}a^{-7}-6z^{7}a^{-9}-27z^{7}a^{-11}-12z^{7}a^{-13}+z^{7}a^{-15}+6z^{6}a^{-6}-17z^{6}a^{-8}-33z^{6}a^{-10}-21z^{6}a^{-12}-11z^{6}a^{-14}+3z^{5}a^{-5}-10z^{5}a^{-7}-8z^{5}a^{-9}+17z^{5}a^{-11}+8z^{5}a^{-13}-4z^{5}a^{-15}+z^{4}a^{-4}-7z^{4}a^{-6}+16z^{4}a^{-8}+32z^{4}a^{-10}+20z^{4}a^{-12}+12z^{4}a^{-14}-2z^{3}a^{-5}+5z^{3}a^{-7}+11z^{3}a^{-9}-2z^{3}a^{-11}-z^{3}a^{-13}+5z^{3}a^{-15}-z^{2}a^{-4}+5z^{2}a^{-6}-9z^{2}a^{-8}-15z^{2}a^{-10}-4z^{2}a^{-12}-4z^{2}a^{-14}-4za^{-9}-za^{-11}+za^{-13}-2za^{-15}-a^{-6}+3a^{-8}+3a^{-10}$
The A2 invariant	Data:K11a320/QuantumInvariant/A2/1,0
The G2 invariant	Data:K11a320/QuantumInvariant/G2/1,0

Further Quantum Invariants

K11a320 Quantum Invariants.

Computer Talk

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["K11a320"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$9t^{2}-27t+37-27t^{-1}+9t^{-2}$

In[5]:=

Conway[K][z]

Out[5]=

$9z^{4}+9z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 109, 4 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$-q^{13}+3q^{12}-7q^{11}+11q^{10}-15q^{9}+17q^{8}-17q^{7}+16q^{6}-11q^{5}+7q^{4}-3q^{3}+q^{2}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$z^{4}a^{-4}+3z^{4}a^{-6}+4z^{4}a^{-8}+z^{4}a^{-10}+z^{2}a^{-4}+4z^{2}a^{-6}+7z^{2}a^{-8}-2z^{2}a^{-10}-z^{2}a^{-12}+a^{-6}+3a^{-8}-3a^{-10}$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$2z^{10}a^{-10}+2z^{10}a^{-12}+6z^{9}a^{-9}+10z^{9}a^{-11}+4z^{9}a^{-13}+9z^{8}a^{-8}+8z^{8}a^{-10}+2z^{8}a^{-12}+3z^{8}a^{-14}+8z^{7}a^{-7}-6z^{7}a^{-9}-27z^{7}a^{-11}-12z^{7}a^{-13}+z^{7}a^{-15}+6z^{6}a^{-6}-17z^{6}a^{-8}-33z^{6}a^{-10}-21z^{6}a^{-12}-11z^{6}a^{-14}+3z^{5}a^{-5}-10z^{5}a^{-7}-8z^{5}a^{-9}+17z^{5}a^{-11}+8z^{5}a^{-13}-4z^{5}a^{-15}+z^{4}a^{-4}-7z^{4}a^{-6}+16z^{4}a^{-8}+32z^{4}a^{-10}+20z^{4}a^{-12}+12z^{4}a^{-14}-2z^{3}a^{-5}+5z^{3}a^{-7}+11z^{3}a^{-9}-2z^{3}a^{-11}-z^{3}a^{-13}+5z^{3}a^{-15}-z^{2}a^{-4}+5z^{2}a^{-6}-9z^{2}a^{-8}-15z^{2}a^{-10}-4z^{2}a^{-12}-4z^{2}a^{-14}-4za^{-9}-za^{-11}+za^{-13}-2za^{-15}-a^{-6}+3a^{-8}+3a^{-10}$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {}

Computer Talk

The above data is available with the Mathematica package KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of May 31, 2006, 14:15:20.091. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["K11a320"];

In[4]:=

{A = Alexander[K][t], J = Jones[K][q]}

KnotTheory::loading: Loading precomputed data in PD4Knots`.

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[4]=

{ $9t^{2}-27t+37-27t^{-1}+9t^{-2}$, $-q^{13}+3q^{12}-7q^{11}+11q^{10}-15q^{9}+17q^{8}-17q^{7}+16q^{6}-11q^{5}+7q^{4}-3q^{3}+q^{2}$ }

In[5]:=

DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]

KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.

KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

Out[5]=

{}

In[6]:=

DeleteCases[ Select[ AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) & ], K ]

KnotTheory::loading: Loading precomputed data in Jones4Knots11`.

Out[6]=

{}

Vassiliev invariants

V2 and V3:

(9, 26)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $36$ $208$ $648$ $1578$ $246$ $7488$ ${\frac {39616}{3}}$ ${\frac {6880}{3}}$ $1808$ $7776$ $21632$ $56808$ $8856$ ${\frac {1125053}{10}}$ ${\frac {11254}{5}}$ ${\frac {222782}{5}}$ ${\frac {1761}{2}}$ ${\frac {58973}{10}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$4 is the signature of K11a320. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ 0 1 2 3 4 5 6 7 8 9 10 11 χ 27                       1 -1 25                     2   2 23                   5 1   -4 21                 6 2     4 19               9 5       -4 17             8 6         2 15           9 9           0 13         7 8             -1 11       4 9               5 9     3 7                 -4 7     4                   4 5 1 3                     -2 3 1                       1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=3$ $i=5$ $r=0$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=1$ ${\mathbb {Z} }^{3}$ $r=2$ ${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=3$ ${\mathbb {Z} }^{7}\oplus {\mathbb {Z} }_{2}^{4}$ ${\mathbb {Z} }^{4}$ $r=4$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{7}$ ${\mathbb {Z} }^{7}$ $r=5$ ${\mathbb {Z} }^{8}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=6$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{8}$ ${\mathbb {Z} }^{8}$ $r=7$ ${\mathbb {Z} }^{6}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=8$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{6}$ ${\mathbb {Z} }^{6}$ $r=9$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}^{5}$ ${\mathbb {Z} }^{5}$ $r=10$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=11$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages. See/edit the Hoste-Thistlethwaite Knot Page master template (intermediate). See/edit the Hoste-Thistlethwaite_Splice_Base (expert). Back to the top.

K11a319 K11a321