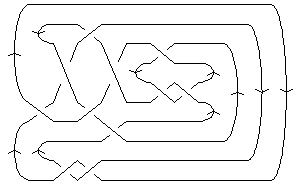
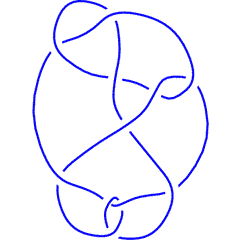
The above data is available with the
Mathematica package
KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in
red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot
5_2) as the notebook
PolynomialInvariantsSession.nb.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
In[3]:=
|
K = Knot["K11n53"];
|
|
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|

|
Out[5]=
|

|
In[6]:=
|
Alexander[K, 2][t]
|
|
|
KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.
|
Out[6]=
|

|
In[7]:=
|
{KnotDet[K], KnotSignature[K]}
|
|
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[8]=
|

|
In[9]:=
|
HOMFLYPT[K][a, z]
|
|
|
KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.
|
Out[9]=
|

|
In[10]:=
|
Kauffman[K][a, z]
|
|
|
KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.
|
Out[10]=
|

|