L11a289

L11a288

L11a290

(Knotscape image)	See the full Thistlethwaite Link Table (up to 11 crossings). Visit L11a289 at Knotilus!

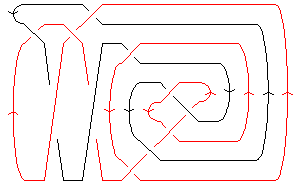
Celtic or pseudo-Celtic linear decorative knot

Decorative variant with big loops at ends

(Also see Detecting a Link Using the Multivariable Alexander Polynomial.)

Link Presentations

[edit Notes on L11a289's Link Presentations]

Planar diagram presentation	X10,1,11,2 X12,4,13,3 X22,12,9,11 X2,9,3,10 X20,14,21,13 X14,7,15,8 X18,16,19,15 X16,6,17,5 X6,18,7,17 X4,19,5,20 X8,22,1,21
Gauss code	{1, -4, 2, -10, 8, -9, 6, -11}, {4, -1, 3, -2, 5, -6, 7, -8, 9, -7, 10, -5, 11, -3}

A Braid Representative
A Morse Link Presentation

Polynomial invariants

Multivariable Alexander Polynomial (in $u$, $v$, $w$, ...)	${\frac {(u-1)(v-1)\left(u^{2}v^{2}-2u^{2}v+u^{2}-2uv^{2}+2uv-2u+v^{2}-2v+1\right)}{u^{3/2}v^{3/2}}}$ (db)
Jones polynomial	$16q^{9/2}-18q^{7/2}+17q^{5/2}-{\frac {1}{q^{5/2}}}-15q^{3/2}+{\frac {3}{q^{3/2}}}+q^{17/2}-4q^{15/2}+8q^{13/2}-12q^{11/2}+10{\sqrt {q}}-{\frac {7}{\sqrt {q}}}$ (db)
Signature	3 (db)
HOMFLY-PT polynomial	$z^{3}a^{-7}+za^{-7}-2z^{5}a^{-5}-5z^{3}a^{-5}-3za^{-5}+z^{7}a^{-3}+4z^{5}a^{-3}+7z^{3}a^{-3}+5za^{-3}-2z^{5}a^{-1}+az^{3}-6z^{3}a^{-1}+2az-5za^{-1}+az^{-1}-a^{-1}z^{-1}$ (db)
Kauffman polynomial	$z^{4}a^{-10}+4z^{5}a^{-9}-2z^{3}a^{-9}+8z^{6}a^{-8}-8z^{4}a^{-8}+3z^{2}a^{-8}+10z^{7}a^{-7}-12z^{5}a^{-7}+6z^{3}a^{-7}-2za^{-7}+8z^{8}a^{-6}-4z^{6}a^{-6}-9z^{4}a^{-6}+4z^{2}a^{-6}+4z^{9}a^{-5}+9z^{7}a^{-5}-34z^{5}a^{-5}+24z^{3}a^{-5}-6za^{-5}+z^{10}a^{-4}+13z^{8}a^{-4}-33z^{6}a^{-4}+16z^{4}a^{-4}+7z^{9}a^{-3}-7z^{7}a^{-3}-24z^{5}a^{-3}+32z^{3}a^{-3}-10za^{-3}+z^{10}a^{-2}+8z^{8}a^{-2}-32z^{6}a^{-2}+28z^{4}a^{-2}-4z^{2}a^{-2}+3z^{9}a^{-1}+az^{7}-5z^{7}a^{-1}-4az^{5}-10z^{5}a^{-1}+6az^{3}+22z^{3}a^{-1}-4az-10za^{-1}+az^{-1}+a^{-1}z^{-1}+3z^{8}-11z^{6}+12z^{4}-3z^{2}-1$ (db)

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$).

\   r    \    j   \ -4 -3 -2 -1 0 1 2 3 4 5 6 7 χ 18                       1 -1 16                     3   3 14                   5 1   -4 12                 7 3     4 10               9 5       -4 8             9 7         2 6           8 9           1 4         7 9             -2 2       5 10               5 0     2 5                 -3 -2   1 5                   4 -4   2                     -2 -6 1                       1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=2$ $i=4$ $r=-4$ ${\mathbb {Z} }$ $r=-3$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-2$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=-1$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{5}$ ${\mathbb {Z} }^{5}$ $r=0$ ${\mathbb {Z} }^{10}\oplus {\mathbb {Z} }_{2}^{5}$ ${\mathbb {Z} }^{7}$ $r=1$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{8}$ ${\mathbb {Z} }^{8}$ $r=2$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=3$ ${\mathbb {Z} }^{7}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=4$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{7}$ ${\mathbb {Z} }^{7}$ $r=5$ ${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}^{5}$ ${\mathbb {Z} }^{5}$ $r=6$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=7$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L11a288 L11a290