Ideal knots
Although all configurations of a given knot are topologically equivalent, there is an Ideal [1] form which minimises the length to diameter ratio Typically there are several local minima of L/D differing by less than 1% - so it can be difficult to distinguish which is the global minimum. There is nothing to prevent a knot having two minima with the same value of L/D and certainly some are very close.
The database of Ideal Knots to 10-crossings gives for each knot the best conformation I have found.
Each is represented by a Fourier series of vectors A[i], B[i], i=1..256 (links also need A[0]), so that
X(t) = A[0]/2 + ∑i A[i]*cos(i.t) + B[i]*sin(i.t)
The file has the following format:-
<DATA Title="..." Author="..." Date="...">
<AB Id="3:1:1" Conway="3" L="16.372861" D=" 1.000000">
<Coeff I=" 1" A=" 0.374743, 0.000000, 0.000000" B=" 0.000000, 0.374482, 0.000000" />
<Coeff I=" 2" A=" 0.938789,-0.600971,-0.000244" B="-0.601135,-0.938461,-0.002035" />
<Coeff I=" 3" A=" 0.000030, 0.000830,-0.283298" B=" 0.000718, 0.000974,-0.442135" />
...
</AB>
The Id is crossing number, number of strings (1) and identifier given by Alexander and Briggs -
also used by Rolfsen (both versions of the Perko pair are given). Thus 5:1:2 is knot 52
The Conway notation is also given. The values of L and D are calculated from a 512 point approximation to this curve.
Zero coefficients are omitted.
To aid comparison of conformations they are standardised to a unique form: -
- the parameter t is linear with string length
- the parameter zero has been rebased, t → t+t0, & rotated so that A[1]=(a,0,0), B[1]=(0,b,0), a > b > 0
- make A[2].x > 0 by selecting t0 or t0+π
- make A[2].y > 0, if necessary, by reversing the string: t → −t (negate all Ay, Az & Bx)
- make A[2].z > 0, if necessary, by reflecting in the X-Y plane (negate all Az & Bz)
- rescale so D = 1
This standardisation is not guaranteed to work always - for example the trefoil given above has A[1].x suspiciously close to B[1].y - if they should be the same the standardisation fails. But this only affects a few knots.
The conformations were obtained using the shrink-on-no-overlap (SONO [1, chapter 2]) algorithm with 512 points. Starting from a stylised layout generated from the Conway notation, this was randomly rearranged before applying SONO. Repeated runs produce about seven different conformations (average for 10 crossing knots), often with very similar values of L/D. It would take several dozen runs for the randomising to find the global minimum for most knots - and even then the wrong one may have been chosen because of the limited accuracy in locating the minimum. Thus, after only a few runs (representing many days of computing), many of the results will only be one of the best local minima.
Compared to Pieranski's results up to 10 crossings [2] many in this database are up to 0.1% worse. This difference arises in the conversion from the point representation used during iteration to the Fourier version: partly because of only using 256 coefficients. Also iteration tends to leave nodes nestled equidistant from both ends of the nearest leash - measuring D by node-to-node distance produces an error of about 0.1%; conversion and standardisation of the Fourier form generally shifts the nodes arbitarily and reduces this error. (N.B. I suspect Pieranski's 10144 [3 1,2 1,2 1-] is derived from Rolfsen's wrongly drawn diagram).
The database of 11-crossing knots is indexed by Hoste-Thistlethwaite id, i.e. 11, a or n (alternating or not) and a number: -
<HT Id="11a1" Conway="2 2 1,2 1 1,2" ...
It is even more difficult to find the global minimum for these knots.
Nevertheless tabulating the knots sorted by L/D reveals many patterns.
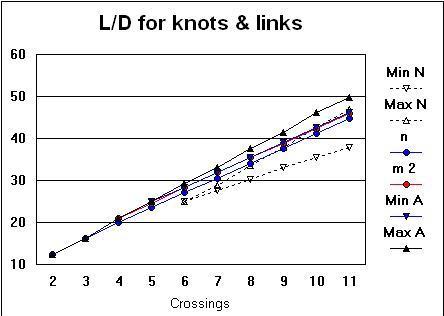
As shown in the graph, for a given crossing number, n, the shortest ideal forms are the non-alternating knots/links comparable to alternating knots of one or two less crossings.
The shortest alternating knot/link is the torus knot with
Conway notation n (L/D ~ 5.66 + 3.57×n),
the next is m 2 (L/D ~ 6.83 + 3.58×n).
Note that the ideal twisted pair ([1, chapter 2, Pieranski]),
which is expected to dominate both n and m 2 for large n, has L/D per crossing of 3.6006
so this should be the asymptotic slope of these curves.
All knots/links up to 11 crossings have L/D < 4.30 + 4.19×n;
thus up to 9 crossings there is no overlap between the ranges of alternating knots/links;
but expect increasing overlap for higher crossing numbers.
Database files: 3-10 crossings Media:Ideal.txt.gz (984kb/5.33Mb)
11 crossings alternating: Media:Ideal_11a.txt.gz (1.52Mb/7.90Mb)
11 crossings non-alternating: Media:Ideal_11n.txt.gz (0.75Mb/3.99Mb)
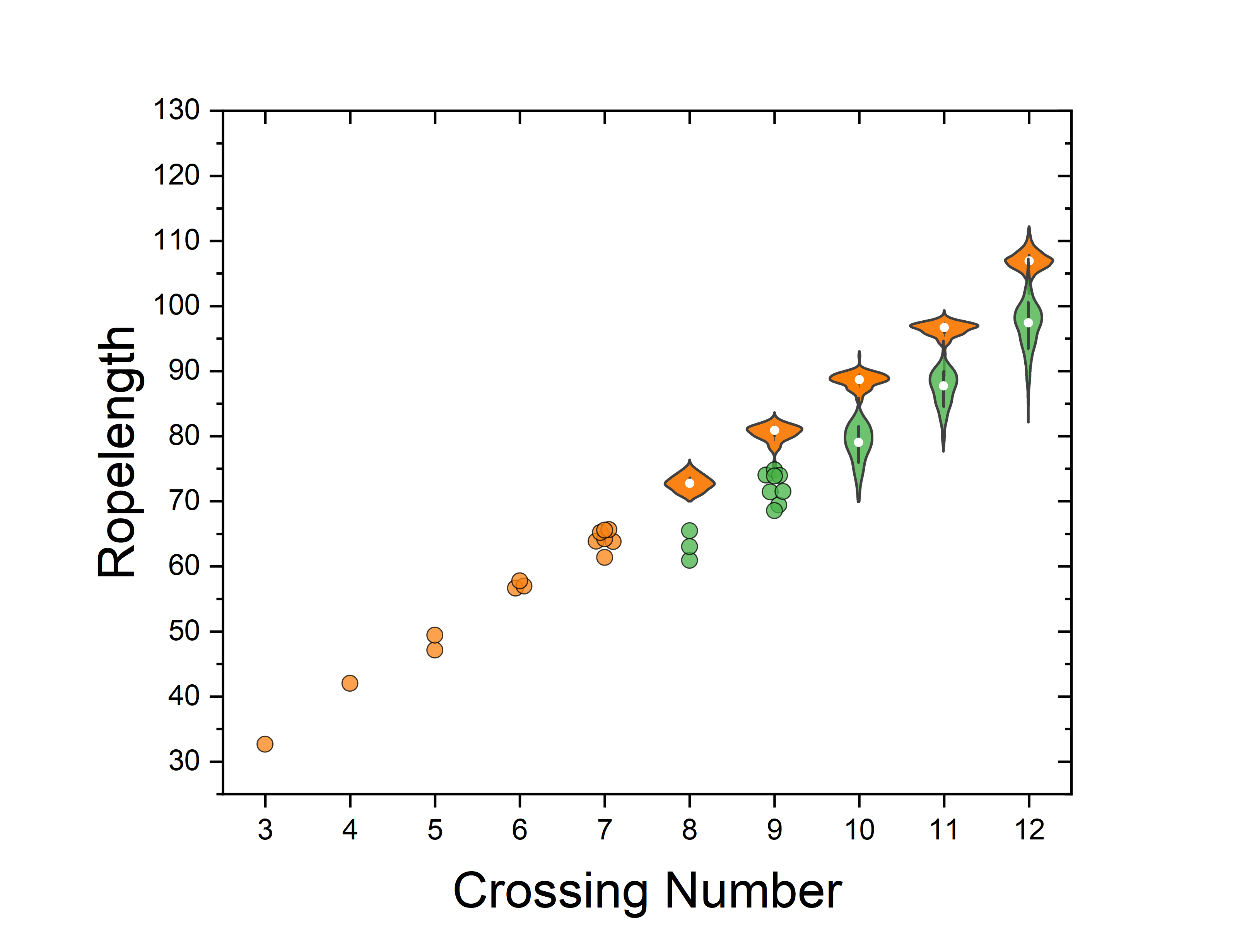
12-Crossing Knots
The ropelength of the 2176 knots with 12 crossings are included in the the uploaded zipped CSV file, along with the space writhe and average crossing number of the tight configuration. This includes 1288 alternating knots and 888 non-alternating knots. The Cartesian coordinates of each knot may be downloaded below and from the Harvard Dataverse. These configurations were computed using Ridgerunner by Alex Klotz and Caleb Anderson, using coordinates generated by Se-Goo Kim at KnotInfo. Note that these computations use the convention that the radius of the knotted tube is 1 instead of the diameter, giving them a factor of 2 difference from the other data on this page. Unlike Brian Gilbert's knots, these do not have a standardized orientation.
Ideal Links
A similar database is provided for links, giving a separate Fourier series for each string. The values of L and D are calculated for 256 (for 2 and 3 strings) or 128 (for 4 and 5 strings) point approximations. Standardisation is applied to the longest string, which is first. The other strings are rebased to make their A[1] and B[1] perpendicular. This is not unique (for instance when strings are similar length, as many are), so comparison of conformations is not easy.
A few Ideal links have strings made from straight lines and unit radius arcs ([2], [.1], [2,2,2,2--]) which were calculated directly. The latter has oval strings of length 2π+2, which form a chain; this does not have a unique conformation as the strings can be moved without changing shape or length. The 12-crossing 6-string link [2,2,2,2,2,2---] is a chain with even more freedom of movement.
The oval of length 2π+2 is the shortest loop which has two strings threaded through it; several links include strings which are nearly this short.
Database files: 2-9 crossings Media:IdealLinks.txt.gz (845kb/5.45Mb)
10 crossings alternating: Media:IdealLinks_10a.txt.gz (1.20Mb/7.23Mb)
10 crossings non-alternating: Media:IdealLinks_10n.txt.gz (0.81Mb/5.13Mb)
11 crossings alternating L11a1 to L11a300: Media:IdealLinks_11a1.txt.gz (1.79Mb/10.02Mb)
11 crossings alternating L11a301 to L11a548: Media:IdealLinks_11a2.txt.gz (1.91Mb/11.48Mb)
11 crossings non-alternating L11n1 to L11n230: Media:IdealLinks_11n1.txt.gz (1.34Mb/7.70Mb)
11 crossings non-alternating L11n231 to L11n459: Media:IdealLinks_11n2.txt.gz (1.73Mb/10.78Mb)
Brian Gilbert
Email: =mailto:brian.gilbert@xtra.co.nz
Ref: [1] Ideal Knots, vol.19 of Series on Knots and Everything, ed: Stasiak, Katritch and Kauffman, World Scientific 1998.
[2] http://fizyka.phys.put.poznan.pl/~pieransk/TablesUpTo9.html