Maximal Thurston-Bennequin number

The Thurston-Bennequin number, usually denoted $tb$, is an invariant of nullhomologous Legendrian knots in contact manifolds, and in particular Legendrian knots in ${\mathbf R}^3$ with the standard contact structure. It is a classical result of [Bennequin] that $tb$ is bounded above for Legendrian knots in any given topological knot type in ${\mathbf R}^3$. The maximal Thurston-Bennequin number of a smooth knot is the largest value of $tb$ among all Legendrian representatives of the knot.

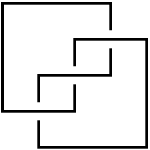
Here is a quick combinatorial definition of maximal Thurston-Bennequin number. Define a rectilinear front diagram to be a knot diagram composed of only horizontal and vertical line segments, such that at any crossing, the horizontal segment lies over the vertical segment. To any rectilinear front diagram $F$, one can associate two integers: the writhe $w(F)$, defined as for any diagram by counting the number of crossings with signs ($+1$ for $(\overcrossing)$ and $-1$ for $(\undercrossing)$), and the cusp number $c(F)$, defined to be the number of locally upper-right corners of $F$. Next define the Thurston-Bennequin number $tb(F)$ to be $w(F)-c(F)$. Finally, the maximal Thurston-Bennequin number of a knot is the maximal value of $tb(F)$ over all rectilinear front diagrams $F$ in the knot type.

For example, the rectilinear front diagram in the figure, which is a right-handed trefoil, has $w=3$, $c=2$, and $tb=1$. In fact, the maximal Thurston-Bennequin number of the right-handed trefoil is $1$.

In the Knot Atlas, maximal Thurston-Bennequin number is given as $[a][b]$, where $a$ and $b$ are the maximal Thurston-Bennequin numbers of the knot and its mirror, respectively. The data has been imported from the KnotInfo site (see their page on the Thurston-Bennequin number).

[Bennequin] ^  D. Bennequin, Entrelacements et équations de Pfaff, Astérisque 107-108 (1983) 87-161.