Maximal Thurston-Bennequin number: Difference between revisions
mNo edit summary |
m (Reverted edits by ErermOnboo (Talk); changed back to last version by Drorbn) |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
The Thurston-Bennequin number, usually denoted <math>tb</math>, is an invariant of nullhomologous Legendrian knots in contact manifolds, and in particular Legendrian knots in <math>{\mathbf R}^3</math> with the standard contact structure. It is a classical result of {{ref|Bennequin}} that <math>tb</math> is bounded above for Legendrian knots in any given topological knot type in <math>{\mathbf R}^3</math>. The maximal Thurston-Bennequin number of a smooth knot is the largest value of <math>tb</math> among all Legendrian representatives of the knot. |
The Thurston-Bennequin number, usually denoted <math>tb</math>, is an invariant of nullhomologous Legendrian knots in contact manifolds, and in particular Legendrian knots in <math>{\mathbf R}^3</math> with the standard contact structure. It is a classical result of {{ref|Bennequin}} that <math>tb</math> is bounded above for Legendrian knots in any given topological knot type in <math>{\mathbf R}^3</math>. The maximal Thurston-Bennequin number of a smooth knot is the largest value of <math>tb</math> among all Legendrian representatives of the knot. |
||
| Line 9: | Line 7: | ||
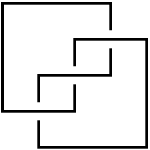
For example, the rectilinear front diagram in the figure, which is a right-handed trefoil, has <math>w=3</math>, <math>c=2</math>, and <math>tb=1</math>. In fact, the maximal Thurston-Bennequin number of the right-handed trefoil is <math>1</math>. |
For example, the rectilinear front diagram in the figure, which is a right-handed trefoil, has <math>w=3</math>, <math>c=2</math>, and <math>tb=1</math>. In fact, the maximal Thurston-Bennequin number of the right-handed trefoil is <math>1</math>. |
||
In the Knot Atlas, maximal Thurston-Bennequin number is given as <math>[a][b]</math>, where <math>a</math> and <math>b</math> are the maximal Thurston-Bennequin numbers of the knot and its mirror, respectively. |
In the Knot Atlas, maximal Thurston-Bennequin number is given as <math>[a][b]</math>, where <math>a</math> and <math>b</math> are the maximal Thurston-Bennequin numbers of the knot and its mirror, respectively. The data has been imported from the KnotInfo site (see [http://www.indiana.edu/~knotinfo/descriptions/thurston_bennequin_number.html their page on the Thurston-Bennequin number]). |
||
{{note|Bennequin}} D. Bennequin, ''Entrelacements et équations de Pfaff'', Astérisque '''107-108''' (1983) 87-161. |
{{note|Bennequin}} D. Bennequin, ''Entrelacements et équations de Pfaff'', Astérisque '''107-108''' (1983) 87-161. |
||
Latest revision as of 07:45, 17 December 2008
The Thurston-Bennequin number, usually denoted , is an invariant of nullhomologous Legendrian knots in contact manifolds, and in particular Legendrian knots in with the standard contact structure. It is a classical result of [Bennequin] that is bounded above for Legendrian knots in any given topological knot type in . The maximal Thurston-Bennequin number of a smooth knot is the largest value of among all Legendrian representatives of the knot.
Here is a quick combinatorial definition of maximal Thurston-Bennequin number. Define a rectilinear front diagram to be a knot diagram composed of only horizontal and vertical line segments, such that at any crossing, the horizontal segment lies over the vertical segment. To any rectilinear front diagram , one can associate two integers: the writhe , defined as for any diagram by counting the number of crossings with signs ( for Failed to parse (unknown function "\overcrossing"): {\displaystyle (\overcrossing)} and for Failed to parse (unknown function "\undercrossing"): {\displaystyle (\undercrossing)} ), and the cusp number , defined to be the number of locally upper-right corners of . Next define the Thurston-Bennequin number to be . Finally, the maximal Thurston-Bennequin number of a knot is the maximal value of over all rectilinear front diagrams in the knot type.
For example, the rectilinear front diagram in the figure, which is a right-handed trefoil, has , , and . In fact, the maximal Thurston-Bennequin number of the right-handed trefoil is .
In the Knot Atlas, maximal Thurston-Bennequin number is given as , where and are the maximal Thurston-Bennequin numbers of the knot and its mirror, respectively. The data has been imported from the KnotInfo site (see their page on the Thurston-Bennequin number).
[Bennequin] ^ D. Bennequin, Entrelacements et équations de Pfaff, Astérisque 107-108 (1983) 87-161.













![{\displaystyle [a][b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96d9f88e3ca30436d7ac2d0cec2408e1f1c3a952)

