Notes for 6 1's three dimensional invariants: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
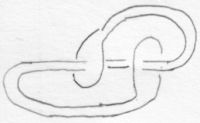
[[6_1]] is a ribbon knot (drawings by Yoko Mizuma): |
[[6_1]] is a ribbon knot (drawings by Yoko Mizuma): |
||
{| align=center |
{| align=center |
||
|[[Image:6_1_As_Ribbon.jpg|thumb| |
|[[Image:6_1_As_Ribbon.jpg|thumb|100px|a ribbon diagram]] |
||
|[[Image:6_1_Ribbon_Sequence.jpg|thumb|isotopy to a ribbon]] |
|[[Image:6_1_Ribbon_Sequence.jpg|thumb|isotopy to a ribbon]] |
||
|} |
|} |
||
[[Image:6_1_is_doubly_slice.jpg|thumb|135px|right|[[6_1]] has two slice disks, by Scott Carter]] Scott Carter notes that 6_1 bounds two distinct slice disks. He says: "this was spoken of in Fox's Example 10, 11, and 12 in ''a Quick Trip through Knot Theory'' ... BTW, the cover of Carter and Saito's ''Knotted Surfaces and Their Diagrams'' contains an illustration of such a slice disk". A picture is on the right. |
|||
Latest revision as of 15:08, 13 July 2020
6_1 is a ribbon knot (drawings by Yoko Mizuma):
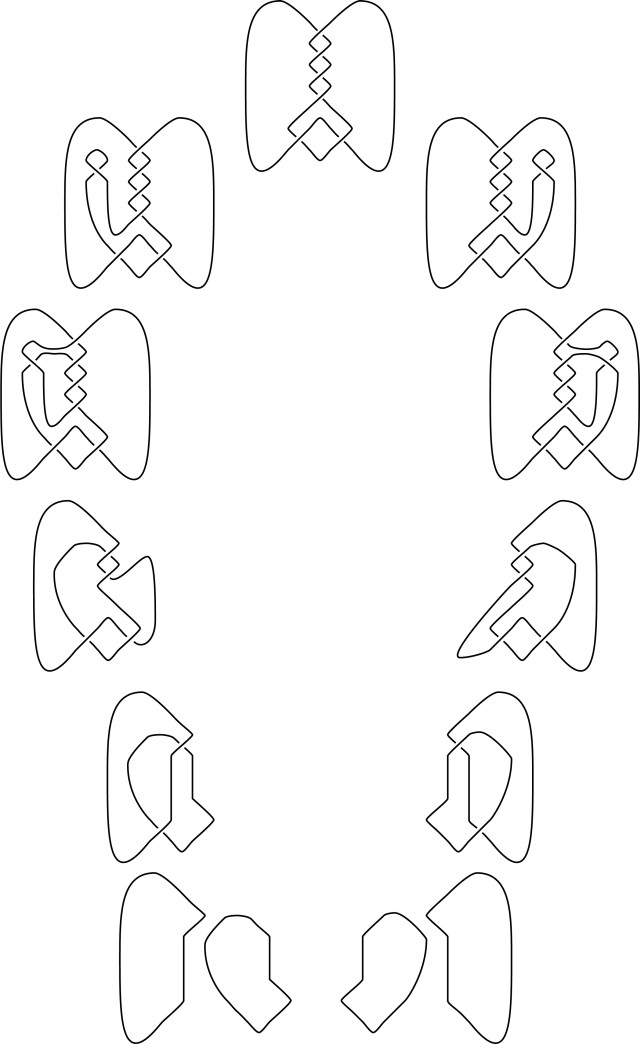
6_1 has two slice disks, by Scott Carter
Scott Carter notes that 6_1 bounds two distinct slice disks. He says: "this was spoken of in Fox's Example 10, 11, and 12 in a Quick Trip through Knot Theory ... BTW, the cover of Carter and Saito's Knotted Surfaces and Their Diagrams contains an illustration of such a slice disk". A picture is on the right.