L11a372: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
<!-- WARNING! WARNING! WARNING! |
<!-- WARNING! WARNING! WARNING! |
||
<!-- This page was generated from the splice |
<!-- This page was generated from the splice base [[Link_Splice_Base]]. Please do not edit! |
||
<!-- You probably want to edit the template referred to immediately below. (See [[Category:Knot Page Template]].) |
<!-- You probably want to edit the template referred to immediately below. (See [[Category:Knot Page Template]].) |
||
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Link_Splice_Base]]. --> |
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Link_Splice_Base]]. --> |
||
<!-- |
<!-- --> |
||
<!-- |
<!-- --> |
||
<!-- WARNING! WARNING! WARNING! |
<!-- WARNING! WARNING! WARNING! |
||
<!-- This page was generated from the splice template [[Link Splice Template]]. Please do not edit! |
<!-- This page was generated from the splice template [[Link Splice Template]]. Please do not edit! |
||
| Line 10: | Line 10: | ||
<!-- The text below simply calls [[Template:Link Page]] setting the values of all the parameters appropriately. |
<!-- The text below simply calls [[Template:Link Page]] setting the values of all the parameters appropriately. |
||
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Link Splice Template]]. --> |
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Link Splice Template]]. --> |
||
<!-- |
<!-- --> |
||
{{Link Page| |
{{Link Page| |
||
n = 11 | |
n = 11 | |
||
t = a | |
t = <nowiki>a</nowiki> | |
||
k = 372 | |
k = 372 | |
||
KnotilusURL = http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-2,3,-6,4,-11,9,-10,8,-5:5,-1,2,-3,6,-4,7,-8,10,-9,11,-7/goTop.html | |
KnotilusURL = http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-2,3,-6,4,-11,9,-10,8,-5:5,-1,2,-3,6,-4,7,-8,10,-9,11,-7/goTop.html | |
||
| Line 44: | Line 44: | ||
<td align=left><pre style="color: red; border: 0px; padding: 0em"><< KnotTheory`</pre></td> |
<td align=left><pre style="color: red; border: 0px; padding: 0em"><< KnotTheory`</pre></td> |
||
</tr> |
</tr> |
||
<tr valign=top><td colspan=2>Loading KnotTheory` (version of August |
<tr valign=top><td colspan=2><nowiki>Loading KnotTheory` (version of August 29, 2005, 15:33:11)...</nowiki></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[2]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>11</nowiki></pre></td></tr> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[2]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Crossings[Link[11, Alternating, 372]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
| ⚫ | |||
< |
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[2]:=</code></td> |
||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>11</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[3]:=</code></td> |
|||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Length[Skeleton[Link[11, Alternating, 372]]]</nowiki></code></td></tr> |
|||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[3]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>2</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[4]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[4]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>PD[X[12, 1, 13, 2], X[2, 13, 3, 14], X[14, 3, 15, 4], X[16, 5, 17, 6], |
|||
X[10, 11, 1, 12], X[4, 15, 5, 16], X[22, 17, 11, 18], |
X[10, 11, 1, 12], X[4, 15, 5, 16], X[22, 17, 11, 18], |
||
X[18, 10, 19, 9], X[20, 8, 21, 7], X[8, 20, 9, 19], X[6, 22, 7, 21]]</nowiki></ |
X[18, 10, 19, 9], X[20, 8, 21, 7], X[8, 20, 9, 19], X[6, 22, 7, 21]]</nowiki></code></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
| ⚫ | |||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[5]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[5]:=</code></td> |
|||
| ⚫ | |||
{5, -1, 2, -3, 6, -4, 7, -8, 10, -9, 11, -7}]</nowiki></ |
{5, -1, 2, -3, 6, -4, 7, -8, 10, -9, 11, -7}]</nowiki></code></td></tr> |
||
</table> |
|||
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[6]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>Show[DrawMorseLink[Link[11, Alternating, 372]]]</nowiki></pre></td></tr><tr><td></td><td align=left>[[Image:L11a372_ML.gif]]</td></tr><tr valign=top><td><tt><font color=blue>Out[6]=</font></tt><td><tt><font color=black>-Graphics-</font></tt></td></tr> |
|||
<table><tr align=left> |
|||
| ⚫ | |||
< |
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[6]:=</code></td> |
||
<td><code style="white-space: pre; color: red; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>Show[DrawMorseLink[Link[11, Alternating, 372]]]</nowiki></code></td></tr> |
|||
<tr align=left><td></td><td>[[Image:L11a372_ML.gif]]</td></tr><tr align=left> |
|||
| ⚫ | |||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[6]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>-Graphics-</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[7]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[7]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki>-5</nowiki></code></td></tr> |
|||
</table> |
|||
<table><tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[8]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[8]:=</code></td> |
|||
| ⚫ | |||
q - ----- + ----- - ----- + ----- - ---- + ---- - ---- + ---- - |
q - ----- + ----- - ----- + ----- - ---- + ---- - ---- + ---- - |
||
17/2 15/2 13/2 11/2 9/2 7/2 5/2 3/2 |
17/2 15/2 13/2 11/2 9/2 7/2 5/2 3/2 |
||
| Line 70: | Line 106: | ||
2 3/2 |
2 3/2 |
||
------- + Sqrt[q] - q |
------- + Sqrt[q] - q |
||
Sqrt[q]</nowiki></ |
Sqrt[q]</nowiki></code></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
| ⚫ | |||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[9]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[9]:=</code></td> |
|||
| ⚫ | |||
1 - q + --- + q + --- + q + q + q + q |
1 - q + --- + q + --- + q + q + q + q |
||
16 12 |
16 12 |
||
q q</nowiki></ |
q q</nowiki></code></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[10]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki> 3 |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[10]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[10]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> 3 |
|||
a a 3 5 7 3 3 3 |
a a 3 5 7 3 3 3 |
||
-(-) + -- - 6 a z + 7 a z + a z - 3 a z - 5 a z + 11 a z + |
-(-) + -- - 6 a z + 7 a z + a z - 3 a z - 5 a z + 11 a z + |
||
| Line 83: | Line 129: | ||
5 3 7 3 5 3 5 5 5 7 5 3 7 5 7 |
5 3 7 3 5 3 5 5 5 7 5 3 7 5 7 |
||
6 a z - 4 a z - a z + 6 a z + 5 a z - a z + a z + a z</nowiki></ |
6 a z - 4 a z - a z + 6 a z + 5 a z - a z + a z + a z</nowiki></code></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[11]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki> 3 |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[11]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[11]:=</code></td> |
|||
<td><code style="white-space: pre; color: black; border: 0px; padding: 0em; background-color: rgb(255,255,255);"><nowiki> 3 |
|||
2 a a 3 5 7 9 2 2 |
2 a a 3 5 7 9 2 2 |
||
-a + - + -- - 9 a z - 11 a z + 2 a z + 2 a z - 2 a z - 2 a z + |
-a + - + -- - 9 a z - 11 a z + 2 a z + 2 a z - 2 a z - 2 a z + |
||
| Line 106: | Line 157: | ||
3 9 5 9 2 10 4 10 |
3 9 5 9 2 10 4 10 |
||
3 a z - 2 a z - a z - a z</nowiki></ |
3 a z - 2 a z - a z - a z</nowiki></code></td></tr> |
||
</table> |
|||
| ⚫ | |||
<table><tr align=left> |
|||
| ⚫ | |||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">In[12]:=</code></td> |
|||
| ⚫ | |||
<tr align=left> |
|||
<td width=70px><code style="color: blue; border: 0px; padding: 0em">Out[12]:=</code></td> |
|||
| ⚫ | |||
-- + -- + ------ + ------ + ------ + ------ + ------ + ------ + |
-- + -- + ------ + ------ + ------ + ------ + ------ + ------ + |
||
6 4 20 7 18 6 16 6 16 5 14 5 14 4 |
6 4 20 7 18 6 16 6 16 5 14 5 14 4 |
||
| Line 119: | Line 175: | ||
2 3 4 4 |
2 3 4 4 |
||
2 t + t + q t</nowiki></ |
2 t + t + q t</nowiki></code></td></tr> |
||
</table> }} |
|||
Revision as of 17:50, 1 September 2005
|
|
|
 (Knotscape image) |
See the full Thistlethwaite Link Table (up to 11 crossings). |
Link Presentations
[edit Notes on L11a372's Link Presentations]
| Planar diagram presentation | X12,1,13,2 X2,13,3,14 X14,3,15,4 X16,5,17,6 X10,11,1,12 X4,15,5,16 X22,17,11,18 X18,10,19,9 X20,8,21,7 X8,20,9,19 X6,22,7,21 |
| Gauss code | {1, -2, 3, -6, 4, -11, 9, -10, 8, -5}, {5, -1, 2, -3, 6, -4, 7, -8, 10, -9, 11, -7} |
| A Braid Representative | {{{braid_table}}} |
| A Morse Link Presentation | 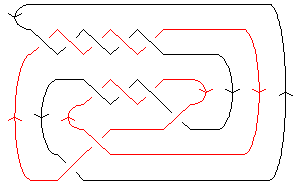
|
Polynomial invariants
| Multivariable Alexander Polynomial (in , , , ...) | (db) |
| Jones polynomial | (db) |
| Signature | -5 (db) |
| HOMFLY-PT polynomial | (db) |
| Kauffman polynomial | (db) |
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). |
|
| Integral Khovanov Homology
(db, data source) |
|
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
Modifying This Page
| Read me first: Modifying Knot Pages
See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top. |
|




































