Help:Editing: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
=== |
=== Usage === |
||
* The easiest way to find a knot/link is to type its name into the search box of the left sidebar and hit "Enter" or click "Go". Examples: |
|||
{| align=center border=1 |
|||
|- align=center |
|||
|type in search box |
|||
|get |
|||
|full [[The Mathematica Package KnotTheory`|<code>KnotTheory`</code>]] notation |
|||
|picture |
|||
|- align=center |
|||
|8 17 |
|||
|the 17th 8-corssing knot in Rolfsen's table, [[8 17|<math>8_{17}</math>]] |
|||
|<code>Knot[8, 17]</code> |
|||
|[[Image:8_17.gif|90px]] |
|||
|- align=center |
|||
|k11a26 |
|||
|the 26th alternating 11-corssing knot in the Hoste-Thistlethwaite table, [[K11a26]] |
|||
|<code>Knot[11, Alternating, 26]</code> |
|||
|[[Image:K11a26.gif|90px]] |
|||
|} |
|||
=== Local Editing Help === |
|||
* Learn about [[how you can contribute]]. |
* Learn about [[how you can contribute]]. |
||
| Line 7: | Line 29: | ||
* Many of the important pages have been categorised, and you can browse these categories by starting at [[:Category:Categories]]. |
* Many of the important pages have been categorised, and you can browse these categories by starting at [[:Category:Categories]]. |
||
=== External Help === |
=== External Editing Help === |
||
* Pages on The Knot Atlas are can and are edited in a similar way to pages on [http://en.wikipedia.org/wiki/Main_Page Wikipedia]. For details, see [http://en.wikipedia.org/wiki/Wikipedia:How_to_edit_a_page Wikipedia:How to edit a page]. |
* Pages on The Knot Atlas are can and are edited in a similar way to pages on [http://en.wikipedia.org/wiki/Main_Page Wikipedia]. For details, see [http://en.wikipedia.org/wiki/Wikipedia:How_to_edit_a_page Wikipedia:How to edit a page]. |
||
Revision as of 13:09, 4 September 2005
Usage
- The easiest way to find a knot/link is to type its name into the search box of the left sidebar and hit "Enter" or click "Go". Examples:
| type in search box | get | full KnotTheory` notation
|
picture |
| 8 17 | the 17th 8-corssing knot in Rolfsen's table, | Knot[8, 17]
|
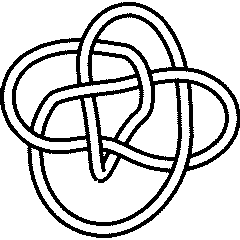
|
| k11a26 | the 26th alternating 11-corssing knot in the Hoste-Thistlethwaite table, K11a26 | Knot[11, Alternating, 26]
|

|
Local Editing Help
- Learn about how you can contribute.
- For help editing manual pages, see How to Edit this Manual....
- For help editing knot pages, see Modifying Knot Pages.
- Some Local Clip Art.
- Many of the important pages have been categorised, and you can browse these categories by starting at Category:Categories.
External Editing Help
- Pages on The Knot Atlas are can and are edited in a similar way to pages on Wikipedia. For details, see Wikipedia:How to edit a page.
Sysadmin Help
- If you need to move this wiki to another server, you'll probably appreciate the katlas installation notes.
- We should automate backup tasks, for now use these backup commands.
