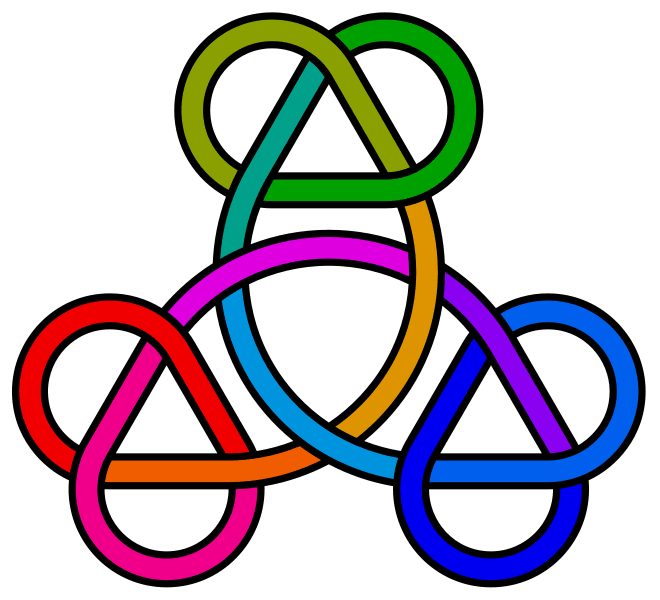3 1 Further Notes and Views: Difference between revisions

From Knot Atlas
Jump to navigationJump to search
(add)
Line 17: Line 17:
}}
}}
{{Knot View Template|
{{Knot View Template|
image = DylansTrefoil_120.jpg |
image = Blue Trefoil Knot.png |
⚫
text = 3D depiction |
⚫
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
}}
}}
⚫
|}


⚫
|}
<div class="NavFrame"><div class="NavHead">Further images...</div>
<div class="NavFrame"><div class="NavHead">Further images...</div>
<div class="NavContent">
<div class="NavContent">
{| style="background: transparent;"
{| style="background: transparent;"
⚫
|- valign=top
⚫
{{Knot View Template|
⚫
image = Trefoil-triquetra-circular-arcs-around-triangle.png |
⚫
text = Ribbons (straight lines and 2/3 circles)|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Triquetra-Vesica.png |
⚫
text = Ribbons (circular arcs)|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Triquetra-tightly-knotted.png |
⚫
text = Tightly-knotted form|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Vodicka triquetra.png |
text = Celtic|
⚫
}}
|- valign=top
|- valign=top
{{Knot View Template|
{{Knot View Template|
Line 39: Line 56:
}}
}}
{{Knot View Template|
{{Knot View Template|
image = Auryn_120.gif |
image = DylansTrefoil_120.jpg |
⚫
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
⚫
text = The NeverEnding Story is a connected sum of two trefoils. [http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html]|
}}
}}
|- valign=top
|- valign=top
Line 58: Line 75:
image = KenyanStone_160.jpg |
image = KenyanStone_160.jpg |
text = A Kenyan Stone [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KenyanStone.html]|
text = A Kenyan Stone [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KenyanStone.html]|
⚫
}}
⚫
|- valign=top
⚫
{{Knot View Template|
⚫
image = Trefoil-triquetra-circular-arcs-around-triangle.png |
⚫
text = Ribbons (straight lines and 2/3 circles)|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Triquetra-Vesica.png |
⚫
text = Ribbons (circular arcs)|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Triquetra-tightly-knotted.png |
⚫
text = Tightly-knotted form|
⚫
}}
⚫
{{Knot View Template|
⚫
image = Vodicka triquetra.png |
⚫
text = Celtic|
}}
}}
|- valign=top
|- valign=top
Line 92: Line 92:
image = RopeTrick_160.jpg |
image = RopeTrick_160.jpg |
text = Mike Hutchings' Rope Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html]|
text = Mike Hutchings' Rope Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html]|
}}
|- valign=top
{{Knot View Template|
image = Auryn_120.gif |
⚫
text = The NeverEnding Story logo is a connected sum of two trefoils. [http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html]|
}}
}}
|}
|}

Revision as of 22:47, 22 March 2010

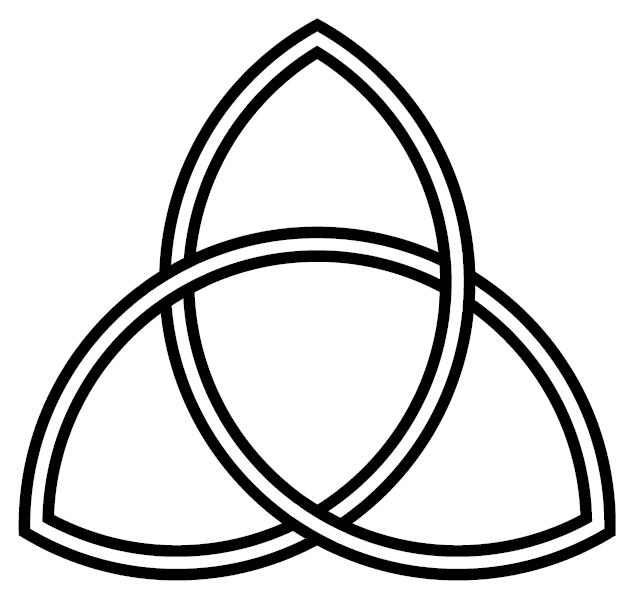
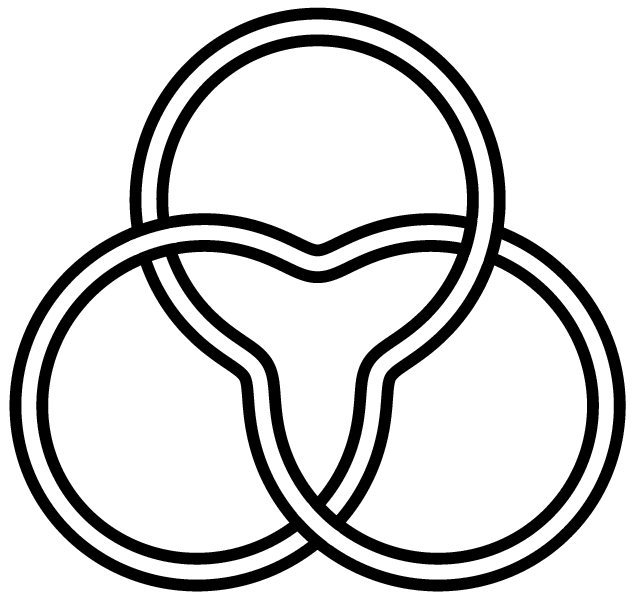
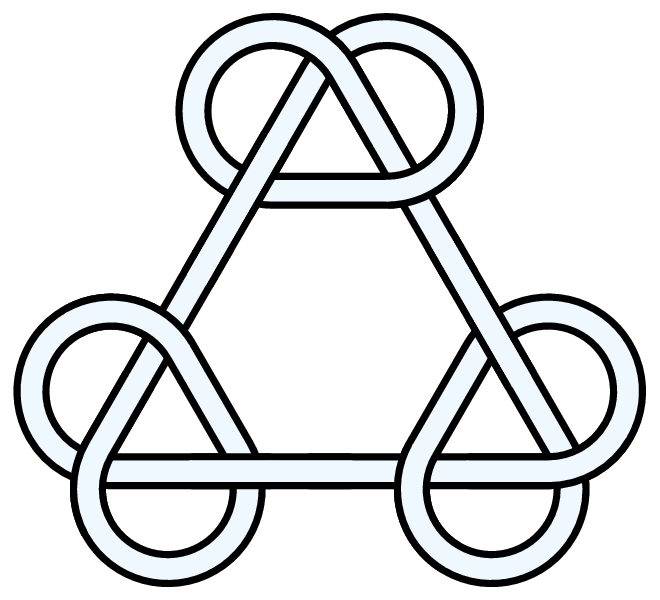
The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:

Logo of Caixa Geral de Depositos, Lisboa [1]
A knot consists of two harts in Kolam [2]
A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity
3D depiction
Further images...
Ribbons (straight lines and 2/3 circles)
Ribbons (circular arcs)
Tightly-knotted form
Celtic
A Knotted Box [3]
A trefoil near the Hollander York Gallery [4]
A Knotted Pencil [5]
Thurston's Trefoil - Figure Eight Trick [6]
Banco Do Brasil [7]
A hagfish tying itself in a knot to escape capture. [8]
One version of the Germanic "Valknut" symbol
A Kenyan Stone [9]
Square depiction
In the form of an architectural trefoil
Polar equation curve.
Mike Hutchings' Rope Trick [10]
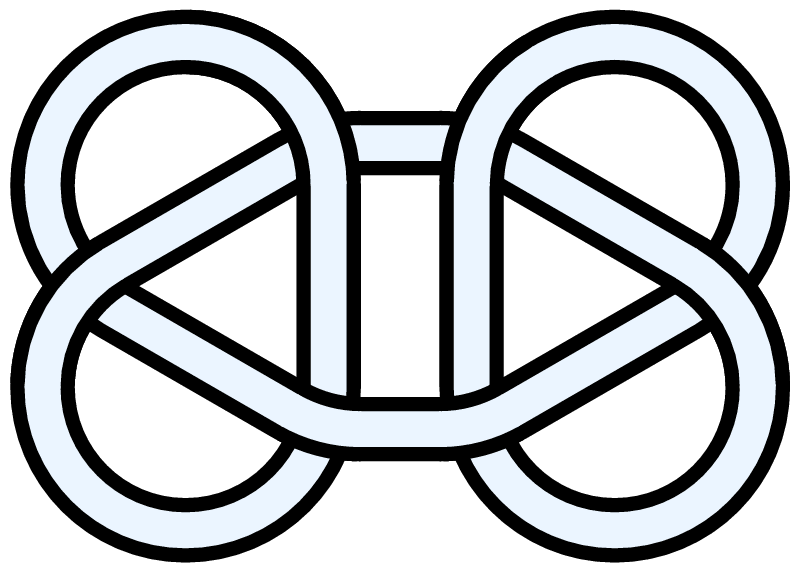
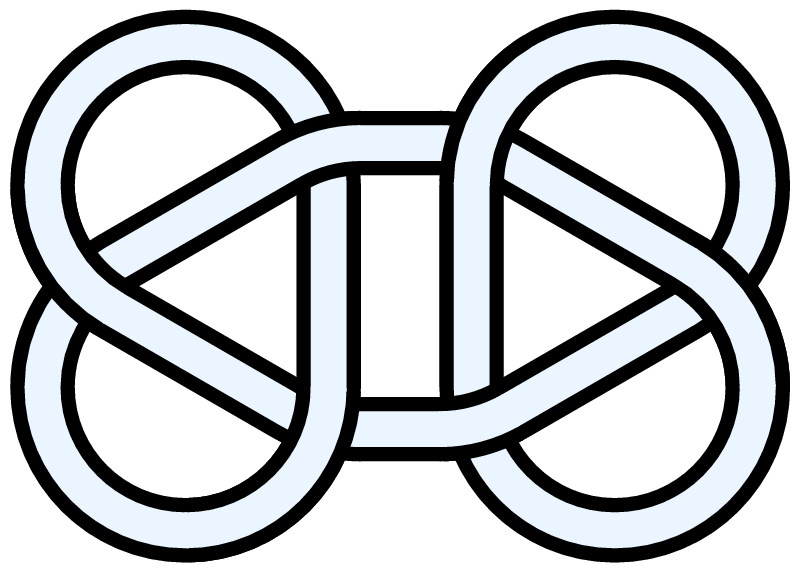
The NeverEnding Story logo is a connected sum of two trefoils. [11]

Non-prime (compound) versions

  • Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

    Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

  • Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

    Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

  • Three trefoils (symmetrical).

    Three trefoils (symmetrical).

  • Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

    Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

  • Three trefoils along a closed loop which itself is knotted as a trefoil.

    Three trefoils along a closed loop which itself is knotted as a trefoil.

For a configuration of two trefoils along a closed loop which is prime, see 10_120.


Retrieved from "https://katlas.org/index.php?title=3_1_Further_Notes_and_Views&oldid=1694381"