Planar Diagrams

The PD notation

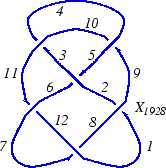
In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols $X_{ijkl}$ where $i$, $j$, $k$ and $l$ are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot on the right is:

$X_{1928}X_{3,10,4,11}X_{5362}X_{7,1,8,12}X_{9,4,10,5}X_{11,7,12,6}.$

(This of course is the Miller Institute knot, the mirror image of the knot 6_2)

(For In[1] see Setup)

In[2]:= ?PD PD[v1, v2, ...] represents a planar diagram whose vertices are v1, v2, .... PD also acts as a "type caster", so for example, PD[K] where K is is a named knot (or link) returns the PD presentation of that knot.

In[3]:= ?X X[i,j,k,l] represents a crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counterclockwise through j, k and l. The (sometimes ambiguous) orientation of the upper strand is determined by the ordering of {j,l}.

Thus, for example, let us compute the determinant of the above knot:

In[4]:= K = PD[X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], X[7,1,8,12], X[9,4,10,5], X[11,7,12,6]];

Out[4]= ${\textrm {Null}}$

In[5]:= Alexander[K][-1]

Out[5]= $-11$