L11a500

L11a499

L11a501

(Knotscape image)	See the full Thistlethwaite Link Table (up to 11 crossings). Visit L11a500 at Knotilus!

Link Presentations

[edit Notes on L11a500's Link Presentations]

Planar diagram presentation	X6172 X12,3,13,4 X22,14,19,13 X20,8,21,7 X10,20,11,19 X16,10,17,9 X14,18,15,17 X8,16,9,15 X18,22,5,21 X2536 X4,11,1,12
Gauss code	{1, -10, 2, -11}, {5, -4, 9, -3}, {10, -1, 4, -8, 6, -5, 11, -2, 3, -7, 8, -6, 7, -9}

A Braid Representative
A Morse Link Presentation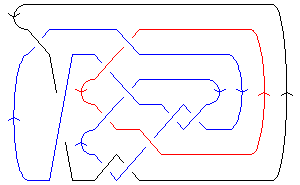

Polynomial invariants

Multivariable Alexander Polynomial (in [math]\displaystyle{ u }[/math], [math]\displaystyle{ v }[/math], [math]\displaystyle{ w }[/math], ...)	[math]\displaystyle{ \frac{(w-1) \left(2 u v w^3-4 u v w^2+3 u v w-u v-2 u w^3+4 u w^2-4 u w-4 v w^3+4 v w^2-2 v w-w^4+3 w^3-4 w^2+2 w\right)}{\sqrt{u} \sqrt{v} w^{5/2}} }[/math] (db)
Jones polynomial	[math]\displaystyle{ -q^8+5 q^7-12 q^6+18 q^5-23 q^4+27 q^3-25 q^2+22 q-14+9 q^{-1} -3 q^{-2} + q^{-3} }[/math] (db)
Signature	2 (db)
HOMFLY-PT polynomial	[math]\displaystyle{ z^6 a^{-2} +z^6 a^{-4} -z^4 a^{-2} +z^4 a^{-4} -z^4 a^{-6} -2 z^4+a^2 z^2-7 z^2 a^{-2} +3 z^2 a^{-4} -z^2+a^2-10 a^{-2} +7 a^{-4} - a^{-6} +3-5 a^{-2} z^{-2} +4 a^{-4} z^{-2} - a^{-6} z^{-2} +2 z^{-2} }[/math] (db)
Kauffman polynomial	[math]\displaystyle{ z^5 a^{-9} +5 z^6 a^{-8} -3 z^4 a^{-8} +12 z^7 a^{-7} -16 z^5 a^{-7} +5 z^3 a^{-7} -2 z a^{-7} + a^{-7} z^{-1} +15 z^8 a^{-6} -23 z^6 a^{-6} +11 z^4 a^{-6} -4 z^2 a^{-6} - a^{-6} z^{-2} +2 a^{-6} +9 z^9 a^{-5} +3 z^7 a^{-5} -30 z^5 a^{-5} +26 z^3 a^{-5} -15 z a^{-5} +5 a^{-5} z^{-1} +2 z^{10} a^{-4} +25 z^8 a^{-4} -60 z^6 a^{-4} +47 z^4 a^{-4} -25 z^2 a^{-4} -4 a^{-4} z^{-2} +14 a^{-4} +14 z^9 a^{-3} -11 z^7 a^{-3} -31 z^5 a^{-3} +52 z^3 a^{-3} -33 z a^{-3} +9 a^{-3} z^{-1} +2 z^{10} a^{-2} +16 z^8 a^{-2} +a^2 z^6-47 z^6 a^{-2} -3 a^2 z^4+53 z^4 a^{-2} +3 a^2 z^2-40 z^2 a^{-2} -5 a^{-2} z^{-2} -a^2+21 a^{-2} +5 z^9 a^{-1} +3 a z^7+z^7 a^{-1} -6 a z^5-24 z^5 a^{-1} +3 a z^3+34 z^3 a^{-1} -20 z a^{-1} +5 a^{-1} z^{-1} +6 z^8-14 z^6+17 z^4-16 z^2-2 z^{-2} +9 }[/math] (db)

Khovanov Homology

The coefficients of the monomials [math]\displaystyle{ t^rq^j }[/math] are shown, along with their alternating sums [math]\displaystyle{ \chi }[/math] (fixed [math]\displaystyle{ j }[/math], alternation over [math]\displaystyle{ r }[/math]).

\   r    \    j   \ -4 -3 -2 -1 0 1 2 3 4 5 6 7 χ 17                       1 -1 15                     4   4 13                   8 1   -7 11                 10 4     6 9               14 9       -5 7             13 9         4 5           12 14           2 3         10 13             -3 1       6 14               8 -1     3 8                 -5 -3     6                   6 -5 1 3                     -2 -7 1                       1

Integral Khovanov Homology (db, data source)

[math]\displaystyle{ \dim{\mathcal G}_{2r+i}\operatorname{KH}^r_{\mathbb Z} }[/math] [math]\displaystyle{ i=1 }[/math] [math]\displaystyle{ i=3 }[/math] [math]\displaystyle{ r=-4 }[/math] [math]\displaystyle{ {\mathbb Z} }[/math] [math]\displaystyle{ {\mathbb Z} }[/math] [math]\displaystyle{ r=-3 }[/math] [math]\displaystyle{ {\mathbb Z}^{3} }[/math] [math]\displaystyle{ r=-2 }[/math] [math]\displaystyle{ {\mathbb Z}^{6}\oplus{\mathbb Z}_2^{3} }[/math] [math]\displaystyle{ {\mathbb Z}^{3} }[/math] [math]\displaystyle{ r=-1 }[/math] [math]\displaystyle{ {\mathbb Z}^{8}\oplus{\mathbb Z}_2^{6} }[/math] [math]\displaystyle{ {\mathbb Z}^{6} }[/math] [math]\displaystyle{ r=0 }[/math] [math]\displaystyle{ {\mathbb Z}^{14}\oplus{\mathbb Z}_2^{8} }[/math] [math]\displaystyle{ {\mathbb Z}^{10} }[/math] [math]\displaystyle{ r=1 }[/math] [math]\displaystyle{ {\mathbb Z}^{13}\oplus{\mathbb Z}_2^{12} }[/math] [math]\displaystyle{ {\mathbb Z}^{12} }[/math] [math]\displaystyle{ r=2 }[/math] [math]\displaystyle{ {\mathbb Z}^{14}\oplus{\mathbb Z}_2^{13} }[/math] [math]\displaystyle{ {\mathbb Z}^{13} }[/math] [math]\displaystyle{ r=3 }[/math] [math]\displaystyle{ {\mathbb Z}^{9}\oplus{\mathbb Z}_2^{14} }[/math] [math]\displaystyle{ {\mathbb Z}^{14} }[/math] [math]\displaystyle{ r=4 }[/math] [math]\displaystyle{ {\mathbb Z}^{9}\oplus{\mathbb Z}_2^{9} }[/math] [math]\displaystyle{ {\mathbb Z}^{10} }[/math] [math]\displaystyle{ r=5 }[/math] [math]\displaystyle{ {\mathbb Z}^{4}\oplus{\mathbb Z}_2^{8} }[/math] [math]\displaystyle{ {\mathbb Z}^{8} }[/math] [math]\displaystyle{ r=6 }[/math] [math]\displaystyle{ {\mathbb Z}\oplus{\mathbb Z}_2^{4} }[/math] [math]\displaystyle{ {\mathbb Z}^{4} }[/math] [math]\displaystyle{ r=7 }[/math] [math]\displaystyle{ {\mathbb Z}_2 }[/math] [math]\displaystyle{ {\mathbb Z} }[/math]

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L11a499 L11a501