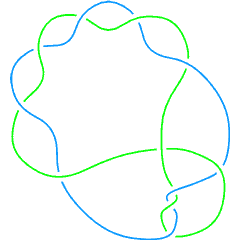
L11a363

L11a362

L11a364

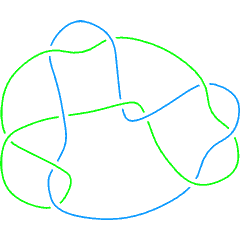(Knotscape image)	See the full Thistlethwaite Link Table (up to 11 crossings). Visit L11a363 at Knotilus!

Link Presentations

[edit Notes on L11a363's Link Presentations]

Planar diagram presentation	X12,1,13,2 X14,4,15,3 X22,14,11,13 X2,11,3,12 X4,22,5,21 X20,10,21,9 X16,6,17,5 X8,18,9,17 X18,8,19,7 X6,20,7,19 X10,16,1,15
Gauss code	{1, -4, 2, -5, 7, -10, 9, -8, 6, -11}, {4, -1, 3, -2, 11, -7, 8, -9, 10, -6, 5, -3}

A Braid Representative
A Morse Link Presentation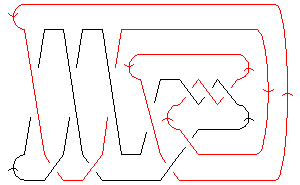

Polynomial invariants

Multivariable Alexander Polynomial (in $u$, $v$, $w$, ...)	$-{\frac {u^{4}v^{2}-u^{4}v+2u^{3}v^{3}-6u^{3}v^{2}+4u^{3}v-u^{3}+u^{2}v^{4}-6u^{2}v^{3}+9u^{2}v^{2}-6u^{2}v+u^{2}-uv^{4}+4uv^{3}-6uv^{2}+2uv-v^{3}+v^{2}}{u^{2}v^{2}}}$ (db)
Jones polynomial	$q^{21/2}-3q^{19/2}+6q^{17/2}-11q^{15/2}+14q^{13/2}-17q^{11/2}+17q^{9/2}-15q^{7/2}+11q^{5/2}-7q^{3/2}+3{\sqrt {q}}-{\frac {1}{\sqrt {q}}}$ (db)
Signature	3 (db)
HOMFLY-PT polynomial	$-z^{5}a^{-3}-2z^{5}a^{-5}-z^{5}a^{-7}+z^{3}a^{-1}-3z^{3}a^{-5}-z^{3}a^{-7}+z^{3}a^{-9}+za^{-1}+2za^{-3}-za^{-7}+za^{-9}+a^{-5}z^{-1}-a^{-7}z^{-1}$ (db)
Kauffman polynomial	$-z^{10}a^{-6}-z^{10}a^{-8}-3z^{9}a^{-5}-6z^{9}a^{-7}-3z^{9}a^{-9}-5z^{8}a^{-4}-7z^{8}a^{-6}-6z^{8}a^{-8}-4z^{8}a^{-10}-5z^{7}a^{-3}-3z^{7}a^{-5}+7z^{7}a^{-7}+2z^{7}a^{-9}-3z^{7}a^{-11}-3z^{6}a^{-2}+5z^{6}a^{-4}+11z^{6}a^{-6}+13z^{6}a^{-8}+9z^{6}a^{-10}-z^{6}a^{-12}-z^{5}a^{-1}+8z^{5}a^{-3}+9z^{5}a^{-5}-3z^{5}a^{-7}+6z^{5}a^{-9}+9z^{5}a^{-11}+5z^{4}a^{-2}-z^{4}a^{-4}-4z^{4}a^{-6}-5z^{4}a^{-8}-4z^{4}a^{-10}+3z^{4}a^{-12}+2z^{3}a^{-1}-5z^{3}a^{-3}-3z^{3}a^{-5}+6z^{3}a^{-7}-6z^{3}a^{-9}-8z^{3}a^{-11}-2z^{2}a^{-2}+z^{2}a^{-6}-z^{2}a^{-10}-2z^{2}a^{-12}-za^{-1}+2za^{-3}-3za^{-5}-5za^{-7}+3za^{-9}+2za^{-11}-a^{-6}+a^{-5}z^{-1}+a^{-7}z^{-1}$ (db)

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , alternation over $r$).

\   r    \    j   \ -2 -1 0 1 2 3 4 5 6 7 8 9 χ 22                       1 -1 20                     2   2 18                   4 1   -3 16                 7 2     5 14               8 5       -3 12             9 6         3 10           8 8           0 8         7 9             -2 6       4 8               4 4     3 7                 -4 2   1 5                   4 0   2                     -2 -2 1                       1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=2$ $i=4$ $r=-2$ ${\mathbb {Z} }$ $r=-1$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=0$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{3}$ $r=1$ ${\mathbb {Z} }^{7}\oplus {\mathbb {Z} }_{2}^{4}$ ${\mathbb {Z} }^{4}$ $r=2$ ${\mathbb {Z} }^{8}\oplus {\mathbb {Z} }_{2}^{7}$ ${\mathbb {Z} }^{7}$ $r=3$ ${\mathbb {Z} }^{9}\oplus {\mathbb {Z} }_{2}^{8}$ ${\mathbb {Z} }^{8}$ $r=4$ ${\mathbb {Z} }^{8}\oplus {\mathbb {Z} }_{2}^{9}$ ${\mathbb {Z} }^{9}$ $r=5$ ${\mathbb {Z} }^{6}\oplus {\mathbb {Z} }_{2}^{8}$ ${\mathbb {Z} }^{8}$ $r=6$ ${\mathbb {Z} }^{5}\oplus {\mathbb {Z} }_{2}^{6}$ ${\mathbb {Z} }^{7}$ $r=7$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}^{4}$ ${\mathbb {Z} }^{4}$ $r=8$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=9$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L11a362 L11a364