File:Brunnian-L10a140.png
From Knot Atlas
Jump to navigationJump to search
Brunnian-L10a140.png (304 × 600 pixels, file size: 12 KB, MIME type: image/png)
Link L10a140 in a form which makes it evident that it is a Brunnian link. The red loop is obviously not linked with either the blue or yellow loops, and if the red loop were absent, then the blue and yellow loops could also be separated from each other (by tucking the big end of the blue loop into the yellow loop and the big end of the yellow loop into the blue loop).
Self-made graphic, declared to be in public domain, generated from the following PostScript source code:
%!
306 396 translate/X{1800 sqrt}def
/A{0 X 3 mul 100 0 180 arc -70 X 3 mul 30 180 225 arc
-70 X 30 45 -45 arcn -70 X neg 30 135 225 arc
-70 X -3 mul 30 45 0 arcn 0 X -3 mul 40 180 360 arc
70 X -3 mul 30 180 135 arcn 70 X neg 30 -45 45 arc
70 X 30 225 135 arcn 70 X 3 mul 30 315 360 arc
closepath
gsave 18 setlinewidth 0 setgray stroke grestore
10 setlinewidth stroke}def
0 0 1 setrgbcolor A
gsave 1 1 0 setrgbcolor 180 rotate A grestore
1 0 0 setrgbcolor -70 -200 70 180 360 arc
-70 200 70 0 180 arc closepath
gsave 18 setlinewidth 0 setgray stroke grestore
10 setlinewidth stroke
18 setlinewidth 0 setgray
-79 -9 moveto 18 18 rlineto stroke
79 -9 moveto -18 18 rlineto stroke
0 X 3 mul 100 80 106 arc stroke
0 X -3 mul 40 240 300 arc stroke
10 setlinewidth 0 0 1 setrgbcolor
-80 -10 moveto 20 20 rlineto stroke
80 -10 moveto -20 20 rlineto stroke
0 X 3 mul 100 78 108 arc stroke
0 X -3 mul 40 236 304 arc stroke showpage
%EOF
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 02:06, 30 April 2013 |  | 304 × 600 (12 KB) | AnonMoos (talk | contribs) | better shapes, fit more compactly |
| 14:18, 29 April 2013 | 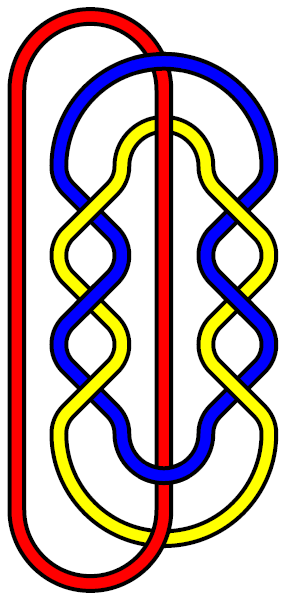 | 285 × 600 (13 KB) | AnonMoos (talk | contribs) | Link L10a140 in a form which makes it evident that it is a Brunnian link. The red loop is obviously not linked to the blue or yellow loops, and if the red loop were absent, then the blue and yellow loops could also be separated from each other (by tu |
You cannot overwrite this file.
File usage
The following 2 pages use this file: