3 1 Further Notes and Views: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 107: | Line 107: | ||
}} |
}} |
||
{{Knot View Template| |
{{Knot View Template| |
||
image = |
image = Impossible trefoil knot Isometric.png | |
||
text = Trefoil knot as impossible object| |
|||
| ⚫ | |||
}} |
}} |
||
|- valign=top |
|- valign=top |
||
| Line 122: | Line 122: | ||
image = DylansTrefoil_120.jpg | |
image = DylansTrefoil_120.jpg | |
||
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]| |
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]| |
||
}} |
|||
{{Knot View Template| |
|||
image = BancoDoBrasil_160.jpg | |
|||
| ⚫ | |||
}} |
}} |
||
|} |
|} |
||
Revision as of 23:46, 2 June 2011
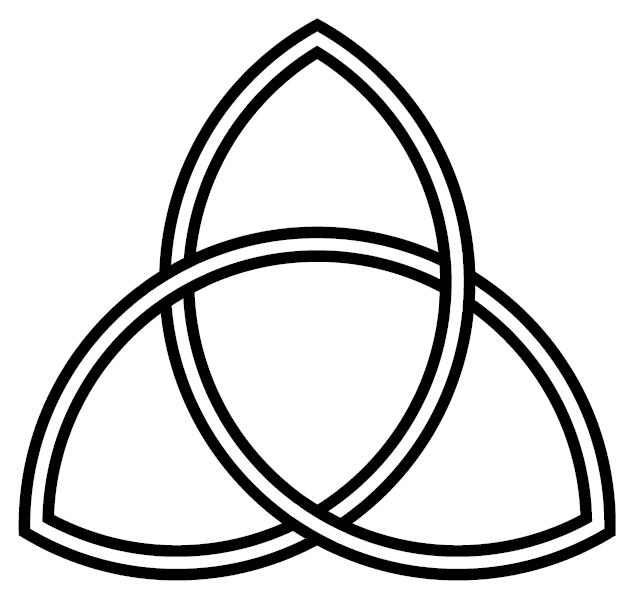
The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:
 Logo of Caixa Geral de Depositos, Lisboa [1] |
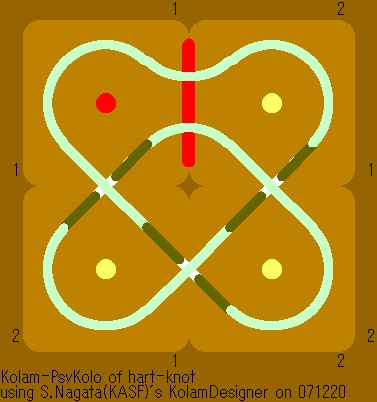 A knot consists of two harts in Kolam [2] |
Further images...
 A Knotted Box [3] |
 A trefoil near the Hollander York Gallery [4] |
 A Knotted Pencil [5] |
|
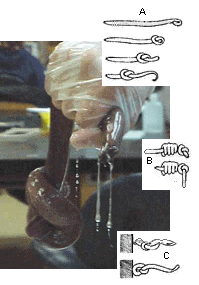 A hagfish tying itself in a knot to escape capture. [6] |
 A Kenyan Stone [7] | ||
 The NeverEnding Story logo is a connected sum of two trefoils. [8] |
 Mike Hutchings' Rope Trick [9] |
 Thurston's Trefoil - Figure Eight Trick [10] |
 Banco Do Brasil [11] |
Non-prime (compound) versions
For configurations of two trefoils along a closed loop which are prime, see 8_15 and 10_120. For a configuration of three trefoils along a closed loop which is prime, see K13a248. For a prime link consisting of two joined trefoils, see L10a108.