10 124 Further Notes and Views: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
No edit summary |
(adding picture of torus knot) |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
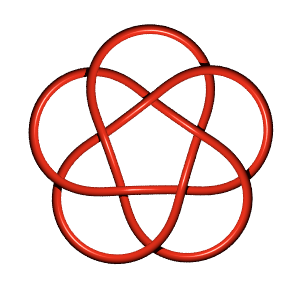
If one takes the symmetric diagram for 10_123 and makes it doubly alternating one gets a diagram for 10_124. That's the torus knot view. There is then a nice representation of the quandle of 10_124 into the dodecahedral quandle |
If one takes the symmetric diagram for [[10_123]] and makes it doubly alternating one gets a diagram for [[10_124]]. That's the torus knot view. There is then a nice representation of the quandle of [[10_124]] into the dodecahedral quandle <math>Q_{30}</math>. See [http://www.maths.warwick.ac.uk/~bjs/add233.html]. |
||
[[10_124]] is not <math>k</math>-colourable for any <math>k</math>. See [[The Determinant and the Signature]]. |
|||
{| style="background: transparent;" |
|||
|- valign=top |
|||
{{Knot View Template| |
|||
image = T53.png | |
|||
text = Torus knot T(5,3) form| |
|||
}} |
|||
|} |
|||
Latest revision as of 08:48, 27 August 2016
If one takes the symmetric diagram for 10_123 and makes it doubly alternating one gets a diagram for 10_124. That's the torus knot view. There is then a nice representation of the quandle of 10_124 into the dodecahedral quandle . See [1].
10_124 is not -colourable for any . See The Determinant and the Signature.