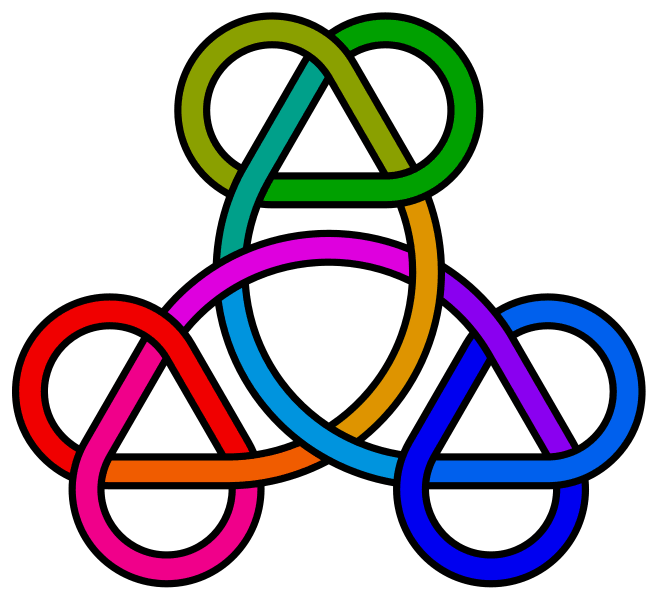3 1 Further Notes and Views: Difference between revisions

From Knot Atlas
Jump to navigationJump to search
No edit summary
 
(7 intermediate revisions by one other user not shown)
Line 40: Line 40:
{{Knot View Template|
{{Knot View Template|
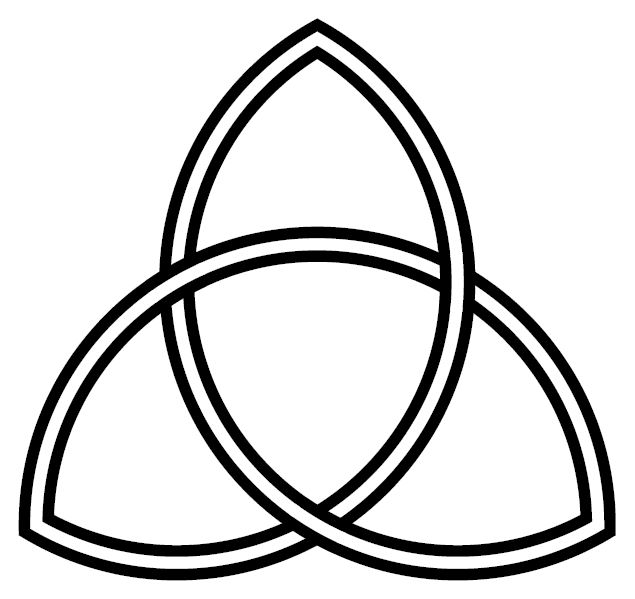
image = Vodicka triquetra.png |
image = Vodicka triquetra.png |
text = Celtic|
text = Celtic-style|
}}
}}
|- valign=top
|- valign=top
Line 52: Line 52:
}}
}}
{{Knot View Template|
{{Knot View Template|
image = KnottedPencil_160.jpg |
image = Three-circles-Trefoil.png |
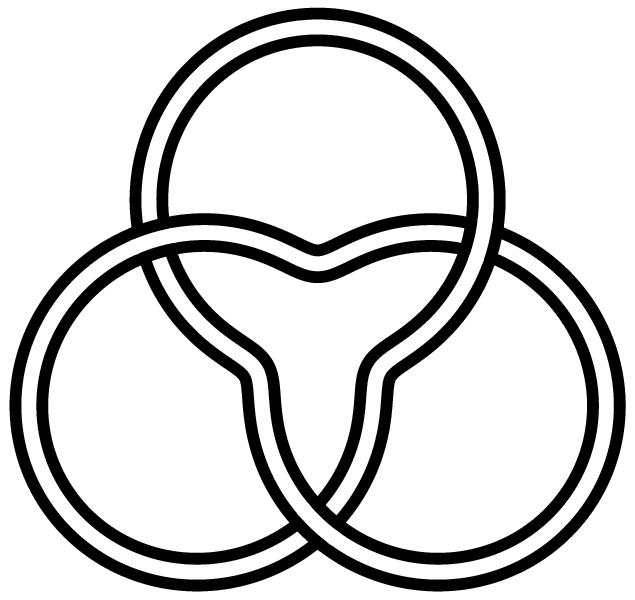
text = Trefoil of three intersecting circles|
⚫
text = A Knotted Pencil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedPencil.html]|
}}
}}
{{Knot View Template|
{{Knot View Template|
Line 95: Line 95:
|- valign=top
|- valign=top
{{Knot View Template|
{{Knot View Template|
image = RopeTrick_160.jpg |
image = Overhand-loop.png |
text = Simple overhand knot of practical knot-tying|
⚫
text = Mike Hutchings' Rope Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html]|
}}
}}
{{Knot View Template|
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
image = Overhand-folded-ribbon-pentagram.png |
text = Tightly folded pentagonal overhand knot|
⚫
text = Banco Do Brasil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html]|
}}
{{Knot View Template|
image = Trefoil-square-centerline.png |
text = Visually fancier square trefoil|
}}
{{Knot View Template|
image = Impossible trefoil knot Isometric.png |
text = Trefoil knot as impossible object|
}}
|- valign=top
{{Knot View Template|
image = TriquetraCaixaGeral.png |
text = Logo of the Caixa Geral de Depósitos with white background|
}}
}}
{{Knot View Template|
{{Knot View Template|
image = Auryn_120.gif |
image = Auryn_120.gif |
text = The NeverEnding Story logo is a connected sum of two trefoils. [http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html]|
text = The NeverEnding Story logo is a connected sum of two trefoils. [http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html]|
}}
{{Knot View Template|
image = RopeTrick_160.jpg |
⚫
text = Mike Hutchings' Rope Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html]|
}}
}}
{{Knot View Template|
{{Knot View Template|
image = DylansTrefoil_120.jpg |
image = DylansTrefoil_120.jpg |
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
}}
|- valign=top
{{Knot View Template|
image = KnottedPencil_160.jpg |
⚫
text = A Knotted Pencil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedPencil.html]|
}}
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
⚫
text = Banco Do Brasil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html]|
}}
}}
|}
|}
Line 120: Line 146:
Image:Celtic-knot-insquare-green-transparentbg.png|Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)
Image:Celtic-knot-insquare-green-transparentbg.png|Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)
Image:Trefoil-of-trefoils.png|Three trefoils along a closed loop which itself is knotted as a trefoil.
Image:Trefoil-of-trefoils.png|Three trefoils along a closed loop which itself is knotted as a trefoil.
Image : multan.jpg|Sum of four trefoils, Multan, Pakistan
</gallery>
</gallery>
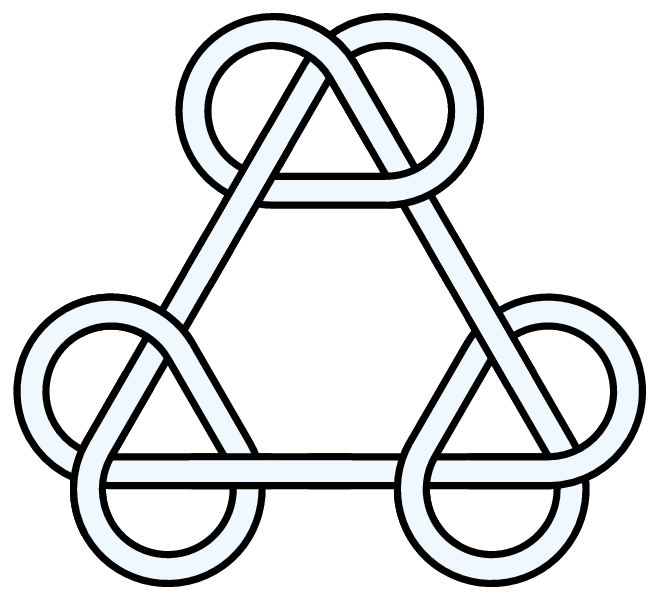
For configurations of two trefoils along a closed loop which are prime, see [[8_15]] and [[10_120]]. For a configuration of three trefoils along a closed loop which is prime, see [[K13a248]]. For a prime link consisting of two joined trefoils, see [[L10a108]].
For configurations of two trefoils along a closed loop which are prime, see [[8_15]] and [[10_120]]. For a configuration of three trefoils along a closed loop which is prime, see [[K13a248]]. For a prime link consisting of two joined trefoils, see [[L10a108]].

Latest revision as of 04:59, 4 June 2018

The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:

Logo of Caixa Geral de Depositos, Lisboa [1]
A knot consists of two harts in Kolam [2]
A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity
3D depiction
Further images...
Trefoil/triquetra without outside corners (made from straight lines and 240° circular arcs)
Triquetra made from circular arc ribbons
Tightly-knotted form
Celtic-style
A Knotted Box [3]
A trefoil near the Hollander York Gallery [4]
Trefoil of three intersecting circles
Trefoil depicted in non-threefold form
3D depiction in non-threefold form
A hagfish tying itself in a knot to escape capture. [5]
One version of the Germanic "Valknut" symbol
A Kenyan Stone [6]
Square depiction
In the form of an architectural trefoil
Polar equation curve.
Alternate Valknut depiction
Simple overhand knot of practical knot-tying
Tightly folded pentagonal overhand knot
Visually fancier square trefoil
Trefoil knot as impossible object
Logo of the Caixa Geral de Depósitos with white background
The NeverEnding Story logo is a connected sum of two trefoils. [7]
Mike Hutchings' Rope Trick [8]
Thurston's Trefoil - Figure Eight Trick [9]
A Knotted Pencil [10]
Banco Do Brasil [11]

Non-prime (compound) versions

  • Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

    Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

  • Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

    Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

  • 3D square knot

    3D square knot

  • Three trefoils (symmetrical).

    Three trefoils (symmetrical).

  • Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

    Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

  • Three trefoils along a closed loop which itself is knotted as a trefoil.

    Three trefoils along a closed loop which itself is knotted as a trefoil.

  • Sum of four trefoils, Multan, Pakistan

    Sum of four trefoils, Multan, Pakistan

For configurations of two trefoils along a closed loop which are prime, see 8_15 and 10_120. For a configuration of three trefoils along a closed loop which is prime, see K13a248. For a prime link consisting of two joined trefoils, see L10a108.


Retrieved from "https://katlas.org/index.php?title=3_1_Further_Notes_and_Views&oldid=1724242"