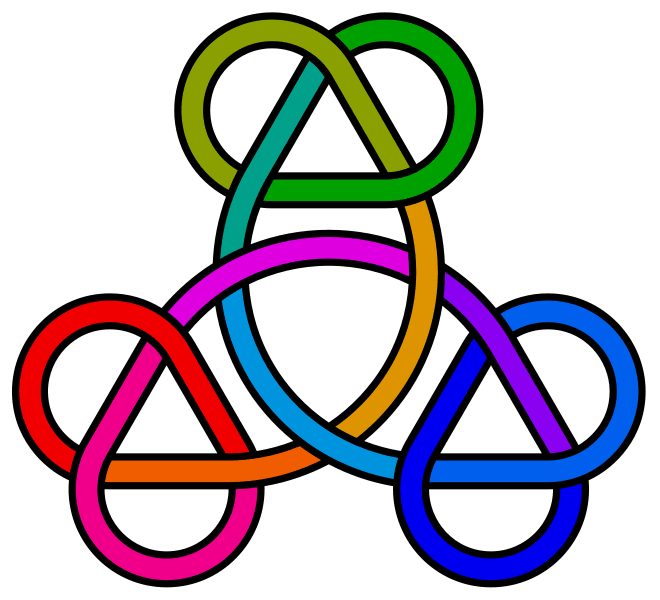3 1 Further Notes and Views: Difference between revisions

From Knot Atlas
Jump to navigationJump to search
No edit summary
 
(44 intermediate revisions by 4 users not shown)
Line 1: Line 1:
The trefoil is perhaps the easiest knot to find in "nature":
The [[3_1|trefoil]] is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [http://en.wikipedia.org/wiki/Triquetra]:


{| style="background: transparent;"
{| style="background: transparent;"
|- valign=top
{{Knot View Template|
{{Knot View Template|
image = RopeTrick_160.jpg |
image = CaixaGeral_160.jpg |
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html |
text = Logo of Caixa Geral de Depositos, Lisboa [http://www.math.toronto.edu/~drorbn/Talks/Oporto-0407/KnotsInLisboa.html]|
text = Mike Hutchings' Rope Trick |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = DylansTrefoil_120.jpg |
image = hart-knot-C.jpg|
text = A knot consists of two harts in Kolam
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html |
[http://intervision.aadau.net/]|
text = Thurston's Trefoil - Figure Eight Trick |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = KenyanStone_160.jpg |
image = Triquetra-Vesica-solid.png |
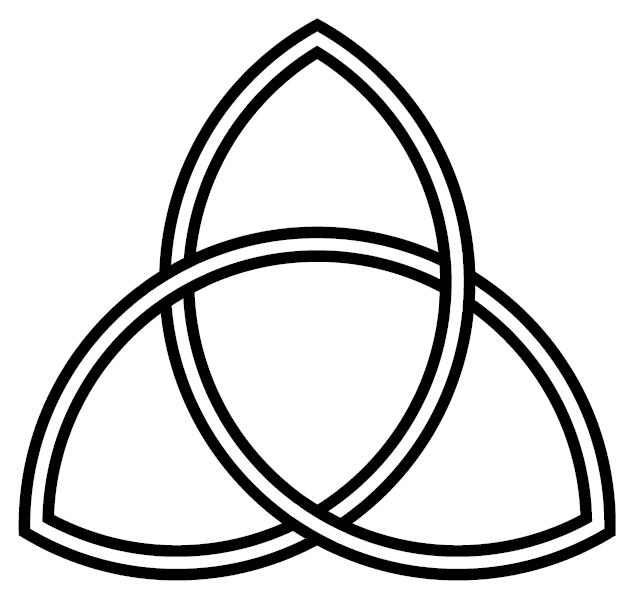
text = A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity|
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KenyanStone.html |
text = A Kenyan Stone |
}}
}}
{{Knot View Template|
|-
image = Blue Trefoil Knot.png |
text = 3D depiction |
}}
|}

<div class="NavFrame"><div class="NavHead">Further images...</div>
<div class="NavContent">
{| style="background: transparent;"
|- valign=top
{{Knot View Template|
image = Trefoil-triquetra-circular-arcs-around-triangle.png |
text = Trefoil/triquetra without outside corners (made from straight lines and 240° circular arcs)|
}}
{{Knot View Template|
image = Triquetra-Vesica.png |
text = Triquetra made from circular arc ribbons|
}}
{{Knot View Template|
image = Triquetra-tightly-knotted.png |
text = Tightly-knotted form|
}}
{{Knot View Template|
image = Vodicka triquetra.png |
text = Celtic-style|
}}
|- valign=top
{{Knot View Template|
{{Knot View Template|
image = KnottedBox_160.jpg |
image = KnottedBox_160.jpg |
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedBox.html |
text = A Knotted Box [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedBox.html]|
text = A Knotted Box |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = HollanderYork_160.jpg |
image = HollanderYork_160.jpg |
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/HollanderYork.html |
text = A trefoil near the Hollander York Gallery [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/HollanderYork.html]|
text = A trefoil near the Hollander York Gallery |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = KnottedPencil_160.jpg |
image = Three-circles-Trefoil.png |
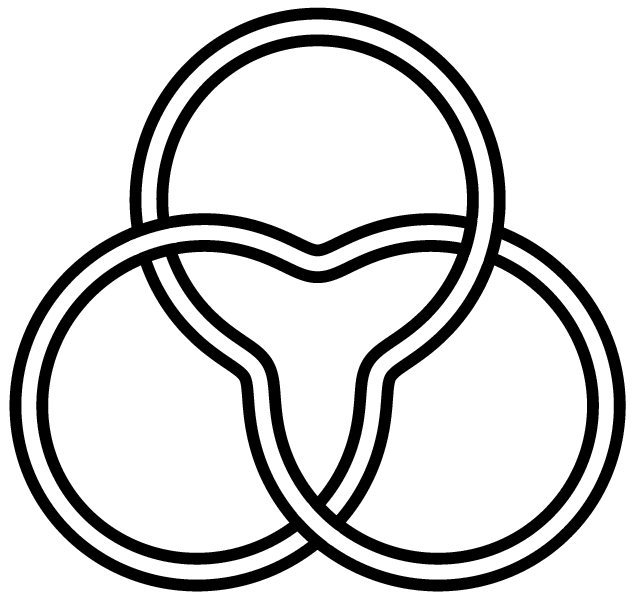
text = Trefoil of three intersecting circles|
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedPencil.html |
}}
text = A Knotted Pencil |
{{Knot View Template|
image = Trefoil-non-3-symm.png |
text = Trefoil depicted in non-threefold form
}}
|- valign=top
{{Knot View Template|
image = One-Twist Trefoil.png |
text = 3D depiction in non-threefold form
}}
{{Knot View Template|
image = hagfish-knotting.gif |
text = A hagfish tying itself in a knot to escape capture. [http://oceanlink.island.net/oinfo/hagfish/hagfish.html]|
}}
{{Knot View Template|
image = Valknut-Symbol-triquetra.png |
text = One version of the Germanic "Valknut" symbol|
}}
{{Knot View Template|
image = KenyanStone_160.jpg |
text = A Kenyan Stone [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KenyanStone.html]|
}}
|- valign=top
{{Knot View Template|
image = Trefoil-square.png |
text = Square depiction|
}}
{{Knot View Template|
image = Trefoil-Triquetra.png |
text = In the form of an architectural trefoil|
}}
{{Knot View Template|
image = Trefoil-triquetra-rhodonea-rose-limacon.png |
text = Polar equation curve.|
}}
{{Knot View Template|
image = Valknut-Symbol-triquetra-alternate.png |
text = Alternate Valknut depiction
}}
|- valign=top
{{Knot View Template|
image = Overhand-loop.png |
text = Simple overhand knot of practical knot-tying|
}}
{{Knot View Template|
image = Overhand-folded-ribbon-pentagram.png |
text = Tightly folded pentagonal overhand knot|
}}
{{Knot View Template|
image = Trefoil-square-centerline.png |
text = Visually fancier square trefoil|
}}
{{Knot View Template|
image = Impossible trefoil knot Isometric.png |
text = Trefoil knot as impossible object|
}}
|- valign=top
{{Knot View Template|
image = TriquetraCaixaGeral.png |
text = Logo of the Caixa Geral de Depósitos with white background|
}}
}}
|-
{{Knot View Template|
{{Knot View Template|
image = Auryn_120.gif |
image = Auryn_120.gif |
link = http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html |
text = The NeverEnding Story logo is a connected sum of two trefoils. [http://www.thealmightyguru.com/Reviews/NeverendingStory/NeverendingStory.html]|
text = The NeverEnding Story is a connected sum of two trefoils. |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = CaixaGeral_160.jpg |
image = RopeTrick_160.jpg |
link = http://www.math.toronto.edu/~drorbn/Talks/Oporto-0407/KnotsInLisboa.html |
text = Mike Hutchings' Rope Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/RopeTrick/index.html]|
text = Logo of Caixa Geral de Depositos, Lisboa |
}}
}}
{{Knot View Template|
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
image = DylansTrefoil_120.jpg |
link = http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html |
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
text = Banco Do Brasil |
}}
}}
|- valign=top
|-
{{Knot View Template|
{{Knot View Template|
image = hagfish-knotting.gif |
image = KnottedPencil_160.jpg |
text = A Knotted Pencil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/KnottedPencil.html]|
link = http://oceanlink.island.net/oinfo/hagfish/hagfish.html |
}}
text = A hagfish tying itself in a knot to escape capture. |
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
text = Banco Do Brasil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html]|
}}
}}
|}
|}

===Non-prime (compound) versions===
<gallery>
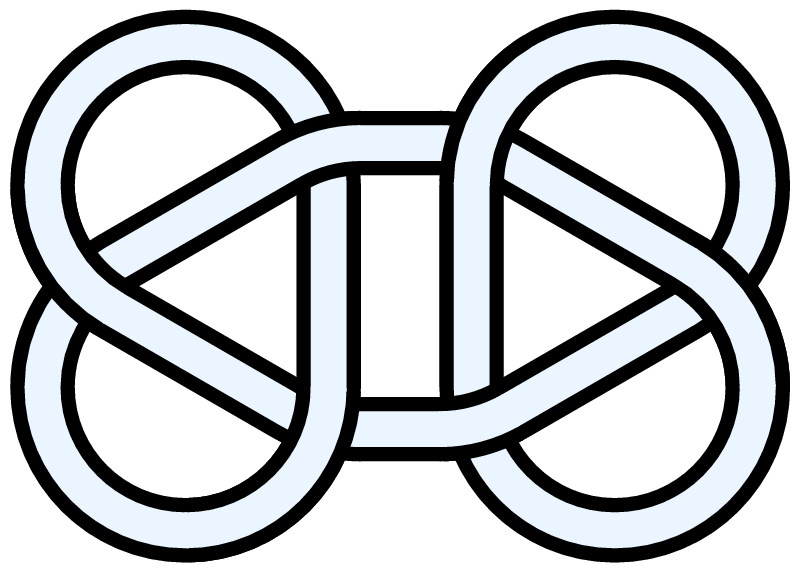
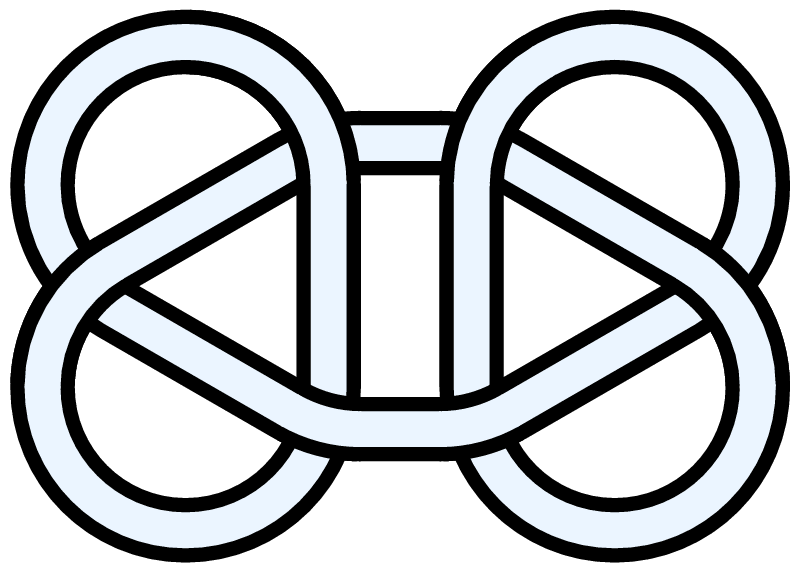
Image:Granny-knot-6-crossings.png|Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).
Image:Square-knot-6-crossings.png|Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)
Image:Blue Square Knot.png|3D square knot
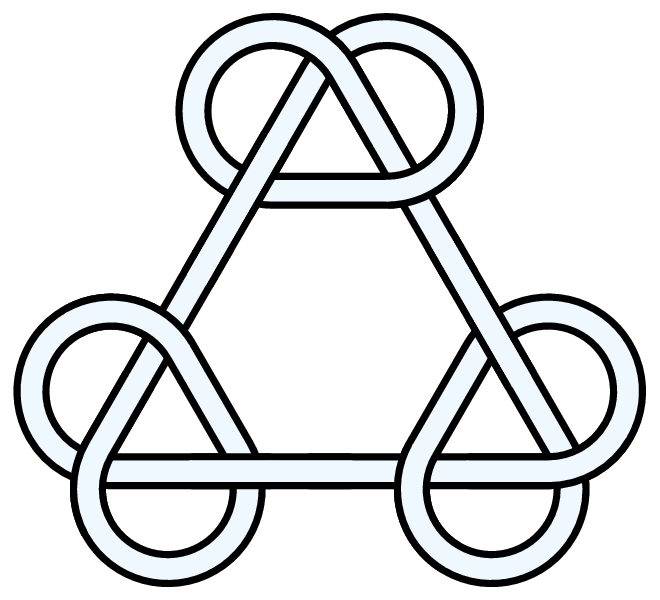
Image:3trefoil-9crossings.gif|Three trefoils (symmetrical).
Image:Celtic-knot-insquare-green-transparentbg.png|Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)
Image:Trefoil-of-trefoils.png|Three trefoils along a closed loop which itself is knotted as a trefoil.
Image : multan.jpg|Sum of four trefoils, Multan, Pakistan
</gallery>
For configurations of two trefoils along a closed loop which are prime, see [[8_15]] and [[10_120]]. For a configuration of three trefoils along a closed loop which is prime, see [[K13a248]]. For a prime link consisting of two joined trefoils, see [[L10a108]].
</div></div>
<br clear=left>

Latest revision as of 04:59, 4 June 2018

The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:

Logo of Caixa Geral de Depositos, Lisboa [1]
A knot consists of two harts in Kolam [2]
A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity
3D depiction
Further images...
Trefoil/triquetra without outside corners (made from straight lines and 240° circular arcs)
Triquetra made from circular arc ribbons
Tightly-knotted form
Celtic-style
A Knotted Box [3]
A trefoil near the Hollander York Gallery [4]
Trefoil of three intersecting circles
Trefoil depicted in non-threefold form
3D depiction in non-threefold form
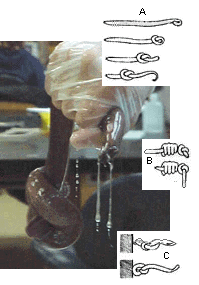A hagfish tying itself in a knot to escape capture. [5]
One version of the Germanic "Valknut" symbol
A Kenyan Stone [6]
Square depiction
In the form of an architectural trefoil
Polar equation curve.
Alternate Valknut depiction
Simple overhand knot of practical knot-tying
Tightly folded pentagonal overhand knot
Visually fancier square trefoil
Trefoil knot as impossible object
Logo of the Caixa Geral de Depósitos with white background
The NeverEnding Story logo is a connected sum of two trefoils. [7]
Mike Hutchings' Rope Trick [8]
Thurston's Trefoil - Figure Eight Trick [9]
A Knotted Pencil [10]
Banco Do Brasil [11]

Non-prime (compound) versions

  • Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

    Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

  • Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

    Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

  • 3D square knot

    3D square knot

  • Three trefoils (symmetrical).

    Three trefoils (symmetrical).

  • Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

    Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

  • Three trefoils along a closed loop which itself is knotted as a trefoil.

    Three trefoils along a closed loop which itself is knotted as a trefoil.

  • Sum of four trefoils, Multan, Pakistan

    Sum of four trefoils, Multan, Pakistan

For configurations of two trefoils along a closed loop which are prime, see 8_15 and 10_120. For a configuration of three trefoils along a closed loop which is prime, see K13a248. For a prime link consisting of two joined trefoils, see L10a108.


Retrieved from "https://katlas.org/index.php?title=3_1_Further_Notes_and_Views&oldid=1724242"