8 18: Difference between revisions
DrorsRobot (talk | contribs) No edit summary |
DrorsRobot (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
<!-- This page was generated from the splice template "Rolfsen_Splice_Template". Please do not edit! --> |
|||
<!-- --> |
<!-- --> |
||
<!-- --> |
<!-- --> |
||
| Line 192: | Line 193: | ||
</table> |
</table> |
||
{| width=100% |
|||
See/edit the [[Rolfsen_Splice_Template]]. |
|align=left|See/edit the [[Rolfsen_Splice_Template]]. |
||
Back to the [[#top|top]]. |
|||
|align=right|{{Knot Navigation Links|ext=gif}} |
|||
|} |
|||
[[Category:Knot Page]] |
[[Category:Knot Page]] |
||
Revision as of 21:05, 29 August 2005
|
|
|
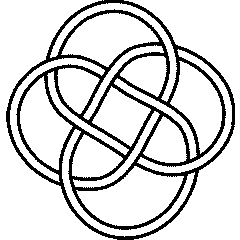
|
Visit 8 18's page at the Knot Server (KnotPlot driven, includes 3D interactive images!)
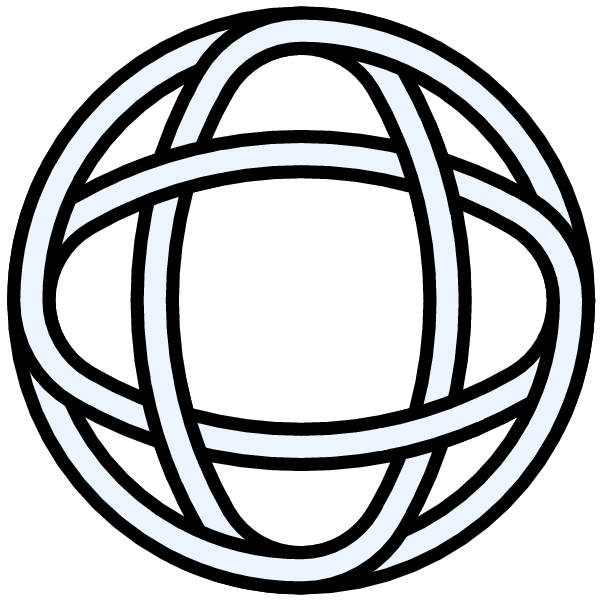
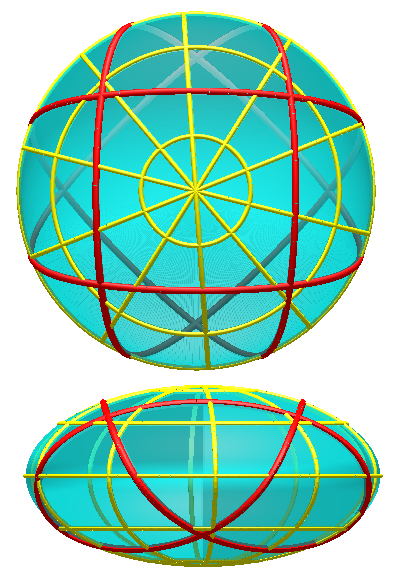
Visit 8 18's page at Knotilus! Visit 8 18's page at the original Knot Atlas! According to Mathematical Models by H. Martyn Cundy and A.P. Rollett, second edition, 1961 (Oxford University Press), p. 57, a flat ribbon or strip can be tightly folded into a heptagonal 8_18 knot (just as it can be tightly folded into a pentagonal trefoil knot). This is the Carrick loop of practical knot tying. The Carrick bend of practical knot tying can be found at . |
 Logo of the International Guild of Knot Tyers [1] |
 A charity logo in Porto [2] |
 A laser cut by Tom Longtin [3] |
||||
|
Knot presentations
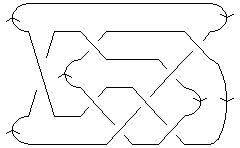
| Planar diagram presentation | X6271 X8394 X16,11,1,12 X2,14,3,13 X4,15,5,16 X10,6,11,5 X12,7,13,8 X14,10,15,9 |
| Gauss code | 1, -4, 2, -5, 6, -1, 7, -2, 8, -6, 3, -7, 4, -8, 5, -3 |
| Dowker-Thistlethwaite code | 6 8 10 12 14 16 2 4 |
| Conway Notation | [8*] |
|
Length is 8, width is 3. Braid index is 3. |
Three dimensional invariants
|
Four dimensional invariants
|
Polynomial invariants
A1 Invariants.
| Weight | Invariant |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
A2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 | |
| 1,1 | |
| 2,0 |
A3 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0 | |
| 1,0,0 | |
| 1,0,1 |
A4 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0,0 | |
| 1,0,0,0 |
B2 Invariants.
| Weight | Invariant |
|---|---|
| 0,1 | |
| 1,0 |
D4 Invariants.
| Weight | Invariant |
|---|---|
| 1,0,0,0 |
G2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 |
.
KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of August 31, 2006, 11:25:27.5625.
|
In[3]:=
|
K = Knot["8 18"];
|
In[4]:=
|
Alexander[K][t]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
In[5]:=
|
Conway[K][z]
|
Out[5]=
|
In[6]:=
|
Alexander[K, 2][t]
|
KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.
|
Out[6]=
|
In[7]:=
|
{KnotDet[K], KnotSignature[K]}
|
Out[7]=
|
{ 45, 0 } |
In[8]:=
|
Jones[K][q]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[8]=
|
In[9]:=
|
HOMFLYPT[K][a, z]
|
KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.
|
Out[9]=
|
In[10]:=
|
Kauffman[K][a, z]
|
KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.
|
Out[10]=
|
"Similar" Knots (within the Atlas)
Same Alexander/Conway Polynomial: {9_24, K11n85, K11n164, ...}
Same Jones Polynomial (up to mirroring, ): {...}
Vassiliev invariants
| V2 and V3: | (1, 0) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). The squares with yellow highlighting are those on the "critical diagonals", where or , where 0 is the signature of 8 18. Nonzero entries off the critical diagonals (if any exist) are highlighted in red. |
|
| Integral Khovanov Homology
(db, data source) |
|
The Coloured Jones Polynomials
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.
| See/edit the Rolfsen_Splice_Template.
Back to the top. |
|
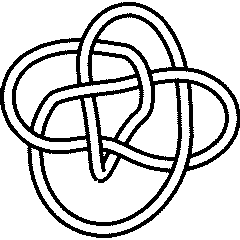
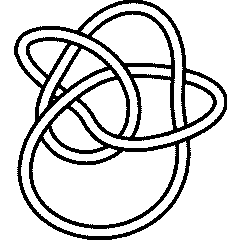


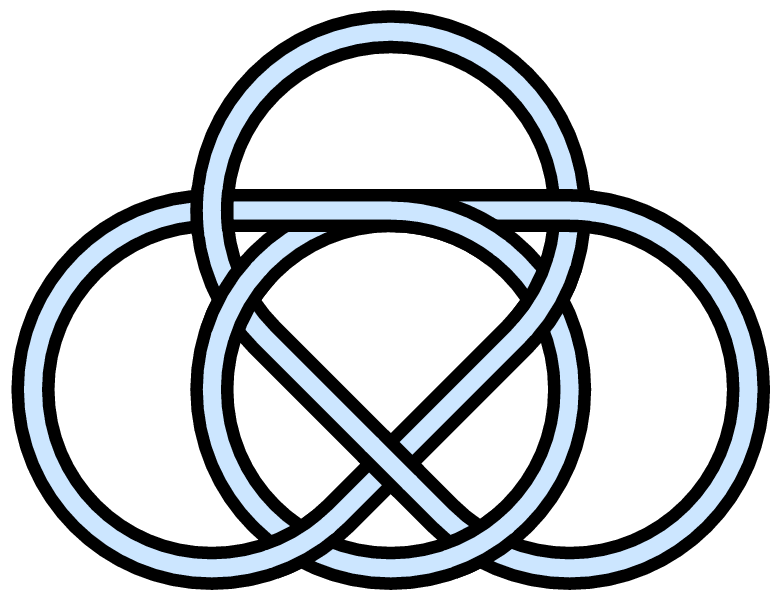










![{\displaystyle [1,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0fcfee68a647afbfbe0440e15fc9fd260abbdc7)













































































