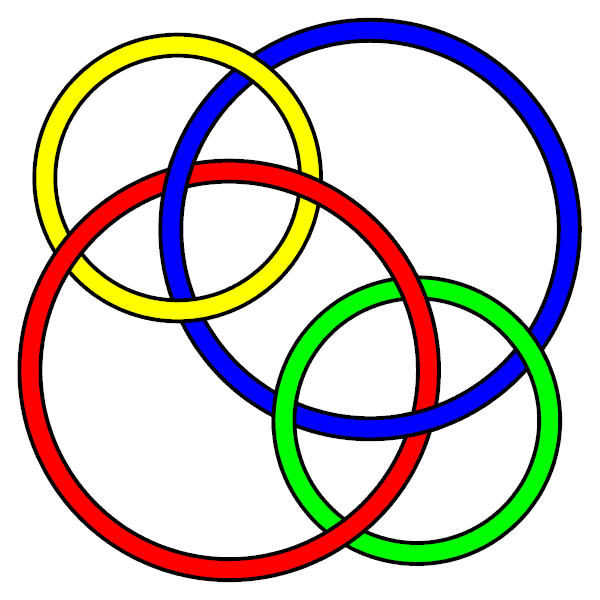User talk:Drorbn

Hello again, Mr. Bar Natan. Thank you for helping me out with my problem. Dr. Conant said that your two examples were similar to his. Anyway, Dr. Conant told me that he became interested in knot theory because you showed up at a presentation he attended. I hope your knot theory career remains a successful one.

Strongbad, 2006-03-14 09:58-05:00

Clarification?

Hi, I just e-mailed you about the "Borromean" bathroom tile, but then realized I could have more easily left a comment here...

Anyway, on the main page, you should probably make it clear that the Rolfsen table is for single-loop knots, while the Thistlewaite table is for multi-loop knots (for people who don't already know that in advance). Thanks. AnonMoos 00:21, 27 Mar 2006 (EST)

P.S., the "Shirt seen in Lisboa" at http://www.math.toronto.edu/~drorbn/Talks/Oporto-0407/KnotsInLisboa.html is actually a partial view of a monochromatic version of the U.S. Bicentennial emblem of 1976. See http://en.wikipedia.org/wiki/Image:Bicentlogo.png

Borromean chain-mail knot?

Which knot number is the "Borromean chain mail" knot? It's not L10a169, but I'm having difficulty determining which it actually is... AnonMoos 15:49, 27 Mar 2006 (EST)

Can't tell without a bit of a search, but I'm running out of time for today... --Drorbn 17:42, 27 Mar 2006 (EST)

Ok, it is L10n107. --Drorbn 21:46, 27 Mar 2006 (EST)

Ok, thanks (of course, I just assumed it was alternating without examining it, sorry). AnonMoos 23:40, 28 Mar 2006 (EST)

Linear decorative knot

Sorry to keep bothering you, but I was looking at the simplest Celtic or pseudo-Celtic linear decorative knot, and it seems to be a real 8-crossing two-loop alternating link (when you shake it, it definitely does not fall apart), but I'm having difficulty relating it to any of the visual depictions on page The Thistlethwaite Link Table L8a1-L8a21... AnonMoos 12:24, 2 Apr 2006 (EDT)

Cool! It is the mirror image of L8a8, and it is not obvious to see that. In fact, I had to run the program KnotTheory` and see that the two have the same (i.e., opposite) invariants.

The Knot Atlas does not distinguish a knot from its mirror, so the picture should go on the L8a8 page. --Drorbn 16:13, 2 Apr 2006 (EDT)

Ok, thanks. It seems that there isn't really currently any program which will take a quasi-arbitrary input diagram and automatically report back "That's link #782 on the list." AnonMoos 22:19, 3 Apr 2006 (EDT)

Another linear decorative knot

I'm having difficulty in relating this to any of the list of alternating 10-crossing two-loop links, thanks... AnonMoos 21:42, 20 Jun 2006 (EDT)

Ouch! That was some strugle for me too, and it underlines the fact that my/our tools for doing such searches are not good enough. First I scanned the link table by hand and found nothing. Then I've quickly entered by hand a DTCode for your link, and it came out to be DTCode[{6, 12, 20, 16, 18}, {2, 4, 10, 8, 14}]. Then I computed the Jones polynomial of that and compared it with the Jones polynomials of all 10 crossings alternating links. Only two links differed from ours by a power of $q$ - L10a31 and L10a101. Of these the first gets ruled out immediately. The second seemed possible, but just to be sure I computed its Multivariable Alexander polynomial and found that it was complete different than the MVA of your link. After flipping the orientation of one of the components of your link so as to get DTCode[{6, 20, 12, 16, 14}, {2, 18, 8, 10, 4}], everything is well.

So the answer is L10a101.

--Drorbn 10:30, 23 Jun 2006 (EDT)

Sorry if I was imposing an excessively fatiguing task on you, but I kind of like to correlate the decorative and/or symbolic motifs. Anyway, I'm already more or less approaching the limits of what has been done in that area with 11 or fewer crossings...

I did download Knotscape, and booted Linux to run it, and that helped me identify Image:Vodicka-3pointed-knot.gif as 10_75, but it seems that nothing except getting into the nitty gritty of the mathematics helps with multi-loop knots (links)...

If two-loop links which are actually inherently symmetrical between the two loops (as L10a101 seems to be) were always portrayed symmetically, that would be helpful. AnonMoos 22:16, 27 Jun 2006 (EDT)