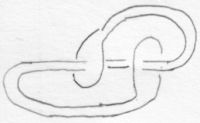
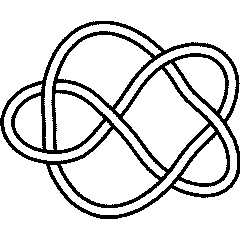6 1: Difference between revisions
m (Reverted edits by ChiceLtvir (Talk); changed back to last version by Scott) |
m (Reverted edits by VivarCasit (Talk); changed back to last version by Drorbn) |
| (One intermediate revision by one other user not shown) | |
(No difference)
| |
Latest revision as of 23:10, 27 May 2009
|
|
|
 (KnotPlot image) |
See the full Rolfsen Knot Table. Visit 6 1's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) |
|
6_1 is also known as "Stevedore's Knot" (see e.g. [1]), and as the pretzel knot P(5,-1,-1). |
Knot presentations
| Planar diagram presentation | X1425 X7,10,8,11 X3948 X9,3,10,2 X5,12,6,1 X11,6,12,7 |
| Gauss code | -1, 4, -3, 1, -5, 6, -2, 3, -4, 2, -6, 5 |
| Dowker-Thistlethwaite code | 4 8 12 10 2 6 |
| Conway Notation | [42] |
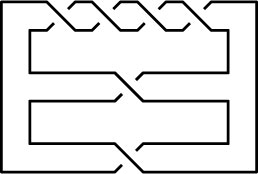
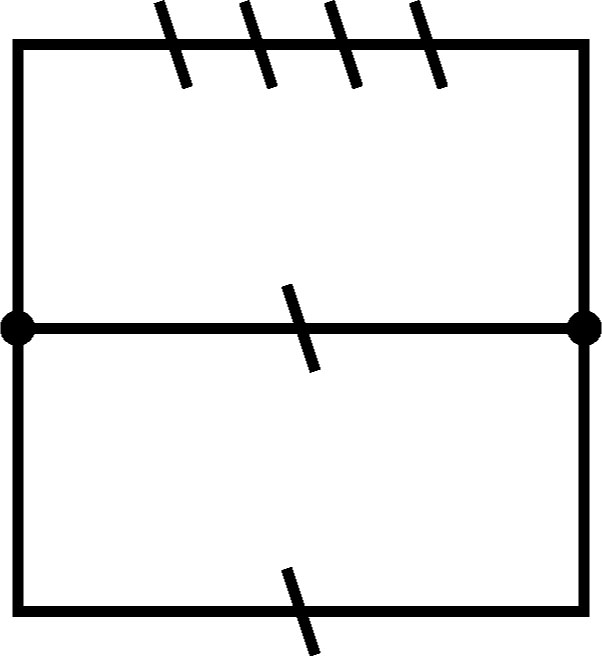
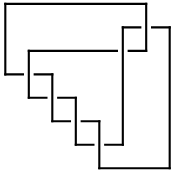
| Minimum Braid Representative | A Morse Link Presentation | An Arc Presentation | ||||
Length is 7, width is 4, Braid index is 4 |

|
 [{8, 5}, {4, 6}, {5, 3}, {2, 4}, {3, 1}, {7, 2}, {6, 8}, {1, 7}] |
[edit Notes on presentations of 6 1]
KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of May 31, 2006, 14:15:20.091.
|
In[3]:=
|
K = Knot["6 1"];
|
In[4]:=
|
PD[K]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
X1425 X7,10,8,11 X3948 X9,3,10,2 X5,12,6,1 X11,6,12,7 |
In[5]:=
|
GaussCode[K]
|
Out[5]=
|
-1, 4, -3, 1, -5, 6, -2, 3, -4, 2, -6, 5 |
In[6]:=
|
DTCode[K]
|
Out[6]=
|
4 8 12 10 2 6 |
(The path below may be different on your system)
In[7]:=
|
AppendTo[$Path, "C:/bin/LinKnot/"];
|
In[8]:=
|
ConwayNotation[K]
|
Out[8]=
|
[42] |
In[9]:=
|
br = BR[K]
|
KnotTheory::credits: The minimum braids representing the knots with up to 10 crossings were provided by Thomas Gittings. See arXiv:math.GT/0401051.
|
Out[9]=
|
In[10]:=
|
{First[br], Crossings[br], BraidIndex[K]}
|
KnotTheory::credits: The braid index data known to KnotTheory` is taken from Charles Livingston's http://www.indiana.edu/~knotinfo/.
|
KnotTheory::loading: Loading precomputed data in IndianaData`.
|
Out[10]=
|
{ 4, 7, 4 } |
In[11]:=
|
Show[BraidPlot[br]]
|
Out[11]=
|
-Graphics- |
In[12]:=
|
Show[DrawMorseLink[K]]
|
KnotTheory::credits: "MorseLink was added to KnotTheory` by Siddarth Sankaran at the University of Toronto in the summer of 2005."
|
KnotTheory::credits: "DrawMorseLink was written by Siddarth Sankaran at the University of Toronto in the summer of 2005."
|

|
Out[12]=
|
-Graphics- |
In[13]:=
|
ap = ArcPresentation[K]
|
Out[13]=
|
ArcPresentation[{8, 5}, {4, 6}, {5, 3}, {2, 4}, {3, 1}, {7, 2}, {6, 8}, {1, 7}] |
In[14]:=
|
Draw[ap]
|

|
Out[14]=
|
-Graphics- |
Three dimensional invariants
|
[edit Notes for 6 1's three dimensional invariants]
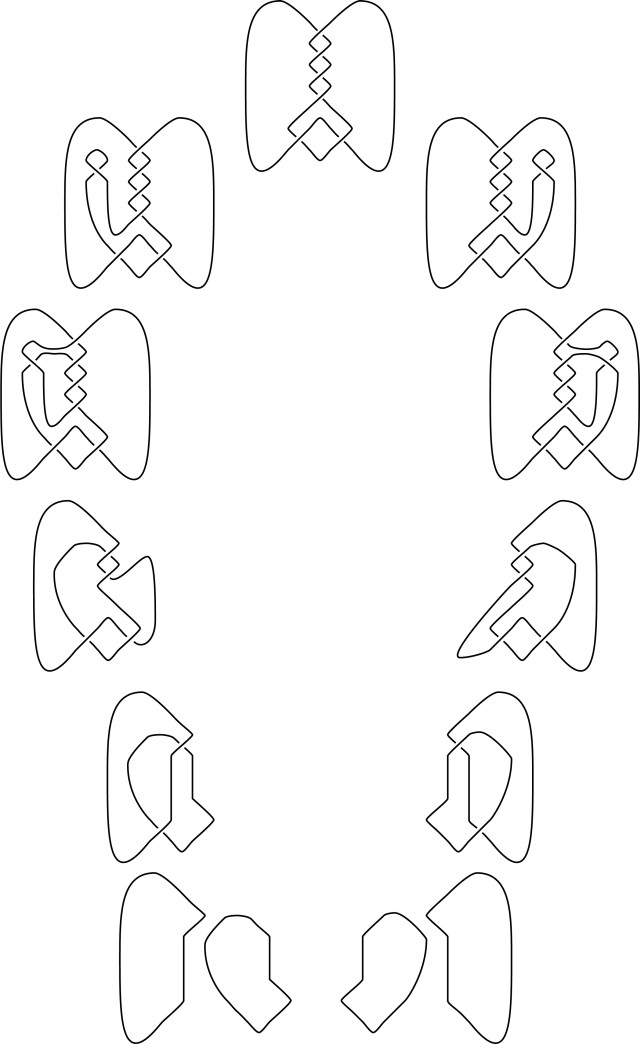 6_1 has two slice disks, by Scott Carter |
Four dimensional invariants
|
Polynomial invariants
A1 Invariants.
| Weight | Invariant |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
A2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 | |
| 1,1 | |
| 2,0 | |
| 3,0 |
A3 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0 | |
| 1,0,0 |
A4 Invariants.
| Weight | Invariant |
|---|---|
| 0,1,0,0 | |
| 1,0,0,0 |
B2 Invariants.
| Weight | Invariant |
|---|---|
| 0,1 | |
| 1,0 |
D4 Invariants.
| Weight | Invariant |
|---|---|
| 1,0,0,0 |
G2 Invariants.
| Weight | Invariant |
|---|---|
| 1,0 |
.
KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of August 31, 2006, 11:25:27.5625.
|
In[3]:=
|
K = Knot["6 1"];
|
In[4]:=
|
Alexander[K][t]
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
Out[4]=
|
In[5]:=
|
Conway[K][z]
|
Out[5]=
|
In[6]:=
|
Alexander[K, 2][t]
|
KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.
|
Out[6]=
|
In[7]:=
|
{KnotDet[K], KnotSignature[K]}
|
Out[7]=
|
{ 9, 0 } |
In[8]:=
|
Jones[K][q]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[8]=
|
In[9]:=
|
HOMFLYPT[K][a, z]
|
KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.
|
Out[9]=
|
In[10]:=
|
Kauffman[K][a, z]
|
KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.
|
Out[10]=
|
"Similar" Knots (within the Atlas)
Same Alexander/Conway Polynomial: {9_46, K11n67, K11n97, K11n139,}
Same Jones Polynomial (up to mirroring, ): {}
KnotTheory`. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting.
(The path below may be different on your system, and possibly also the KnotTheory` date)
In[1]:=
|
AppendTo[$Path, "C:/drorbn/projects/KAtlas/"];
<< KnotTheory`
|
Loading KnotTheory` version of May 31, 2006, 14:15:20.091.
|
In[3]:=
|
K = Knot["6 1"];
|
In[4]:=
|
{A = Alexander[K][t], J = Jones[K][q]}
|
KnotTheory::loading: Loading precomputed data in PD4Knots`.
|
KnotTheory::loading: Loading precomputed data in Jones4Knots`.
|
Out[4]=
|
{ , } |
In[5]:=
|
DeleteCases[Select[AllKnots[], (A === Alexander[#][t]) &], K]
|
KnotTheory::loading: Loading precomputed data in DTCode4KnotsTo11`.
|
KnotTheory::credits: The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.
|
Out[5]=
|
{9_46, K11n67, K11n97, K11n139,} |
In[6]:=
|
DeleteCases[
Select[
AllKnots[],
(J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q]) &
],
K
]
|
KnotTheory::loading: Loading precomputed data in Jones4Knots11`.
|
Out[6]=
|
{} |
Vassiliev invariants
| V2 and V3: | (-2, 1) |
| V2,1 through V6,9: |
|
V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.
Khovanov Homology
| The coefficients of the monomials are shown, along with their alternating sums (fixed , alternation over ). The squares with yellow highlighting are those on the "critical diagonals", where or , where 0 is the signature of 6 1. Nonzero entries off the critical diagonals (if any exist) are highlighted in red. |
|
| Integral Khovanov Homology
(db, data source) |
|
The Coloured Jones Polynomials
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
Computer Talk
Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session, or any of the Computer Talk sections above.
Modifying This Page
| Read me first: Modifying Knot Pages
See/edit the Rolfsen Knot Page master template (intermediate). See/edit the Rolfsen_Splice_Base (expert). Back to the top. |
|