L6a1

L5a1

L6a2

	Visit L6a1's page at Knotilus! Visit ${\textrm {If}}[{\textrm {AlternatingQ}}({\textrm {Link}}(6,{\textrm {Alternating}},1)),a,n]$1.html L6a1's page at the original Knot Atlas!
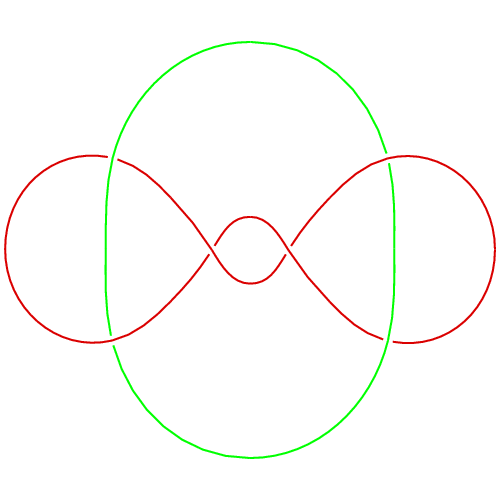
	L6a1 is $6_{3}^{2}$ in the Rolfsen table of links.

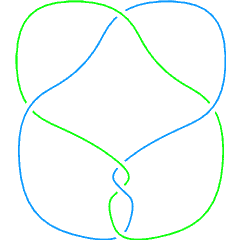
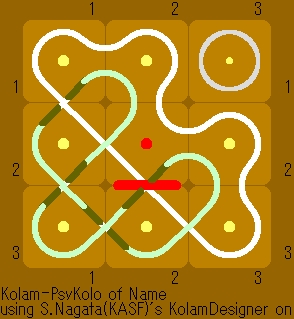A kolam with two cycles/components[1]	Depiction with two eights interlaced	Mongolian ornament ; the two eights are horizontal
Another one, sum of two L6a1	Another depiction

Knot presentations

Planar diagram presentation	X6172 X10,3,11,4 X12,8,5,7 X8,12,9,11 X2536 X4,9,1,10
Gauss code	{1, -5, 2, -6}, {5, -1, 3, -4, 6, -2, 4, -3}

Polynomial invariants

Multivariable Alexander Polynomial (in $u$, $v$, $w$, ...)	${\frac {uv-2u-2v+1}{{\sqrt {u}}{\sqrt {v}}}}$ (db)
Jones polynomial	$-{\frac {1}{q^{9/2}}}+{\frac {1}{q^{7/2}}}-{\frac {3}{q^{5/2}}}-q^{3/2}+{\frac {2}{q^{3/2}}}+2{\sqrt {q}}-{\frac {2}{\sqrt {q}}}$ (db)
Signature	-1 (db)
HOMFLY-PT polynomial	$a^{5}z^{-1}-2za^{3}-a^{3}z^{-1}+z^{3}a+za-za^{-1}$ (db)
Kauffman polynomial	$a^{5}z^{3}-2a^{5}z+a^{5}z^{-1}+a^{4}z^{4}-a^{4}+a^{3}z^{5}-a^{3}z+a^{3}z^{-1}+3a^{2}z^{4}-3a^{2}z^{2}+az^{5}+z^{3}a^{-1}-za^{-1}+2z^{4}-3z^{2}$ (db)

Vassiliev invariants

V2 and V3:

(0, $-{\frac {53}{24}}$)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 Data:L6a1/V 2,1 Data:L6a1/V 3,1 Data:L6a1/V 4,1 Data:L6a1/V 4,2 Data:L6a1/V 4,3 Data:L6a1/V 5,1 Data:L6a1/V 5,2 Data:L6a1/V 5,3 Data:L6a1/V 5,4 Data:L6a1/V 6,1 Data:L6a1/V 6,2 Data:L6a1/V 6,3 Data:L6a1/V 6,4 Data:L6a1/V 6,5 Data:L6a1/V 6,6 Data:L6a1/V 6,7 Data:L6a1/V 6,8 Data:L6a1/V 6,9

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$-1 is the signature of L6a1. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ -4 -3 -2 -1 0 1 2 χ 4             1 1 2           1   -1 0         1 1   0 -2       2 2     0 -4     1         1 -6     2         2 -8 1 1           0 -10 1             1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=-2$ $i=0$ $r=-4$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=-3$ ${\mathbb {Z} }$ $r=-2$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-1$ ${\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=0$ ${\mathbb {Z} }^{2}$ ${\mathbb {Z} }$ $r=1$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=2$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

${\textrm {Include}}({\textrm {ColouredJonesM.mhtml}})$

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 17, 2005, 14:44:34)...
In[2]:=	Crossings[Link[6, Alternating, 1]]
Out[2]=	6
In[3]:=	PD[Link[6, Alternating, 1]]
Out[3]=	PD[X[6, 1, 7, 2], X[10, 3, 11, 4], X[12, 8, 5, 7], X[8, 12, 9, 11], X[2, 5, 3, 6], X[4, 9, 1, 10]]
In[4]:=	GaussCode[Link[6, Alternating, 1]]
Out[4]=	GaussCode[{1, -5, 2, -6}, {5, -1, 3, -4, 6, -2, 4, -3}]
In[5]:=	BR[Link[6, Alternating, 1]]
Out[5]=	BR[Link[6, Alternating, 1]]
In[6]:=	alex = Alexander[Link[6, Alternating, 1]][t]
Out[6]=	ComplexInfinity
In[7]:=	Conway[Link[6, Alternating, 1]][z]
Out[7]=	ComplexInfinity
In[8]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[8]=	{}
In[9]:=	{KnotDet[Link[6, Alternating, 1]], KnotSignature[Link[6, Alternating, 1]]}
Out[9]=	{Infinity, -1}
In[10]:=	J=Jones[Link[6, Alternating, 1]][q]
Out[10]=	-(9/2) -(7/2) 3 2 2 3/2 -q + q - ---- + ---- - ------- + 2 Sqrt[q] - q 5/2 3/2 Sqrt[q] q q
In[11]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[11]=	{}
In[12]:=	A2Invariant[Link[6, Alternating, 1]][q]
Out[12]=	-16 2 -12 2 2 -6 -4 -2 2 6 q + --- + q + --- + -- + q + q - q - q + q 14 10 8 q q q
In[13]:=	Kauffman[Link[6, Alternating, 1]][a, z]
Out[13]=	3 5 3 4 a a z 3 5 2 2 2 z 5 3 4 a - -- - -- + - + a z + 2 a z + 3 z + 3 a z - -- - a z - 2 z - z z a a 2 4 4 4 5 3 5 3 a z - a z - a z - a z
In[14]:=	{Vassiliev[2][Link[6, Alternating, 1]], Vassiliev[3][Link[6, Alternating, 1]]}
Out[14]=	53 {0, -(--)} 24
In[15]:=	Kh[Link[6, Alternating, 1]][q, t]
Out[15]=	1 1 1 + Alternating + ---------------- + --------------- + 4 10 4 8 Alternating q Alternating q 1 2 1 2 --------------- + --------------- + --------------- + -- + 3 8 2 6 2 4 2 Alternating q Alternating q Alternating q q 2 2 2 4 -------------- + Alternating q + Alternating q 2 Alternating q