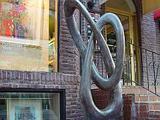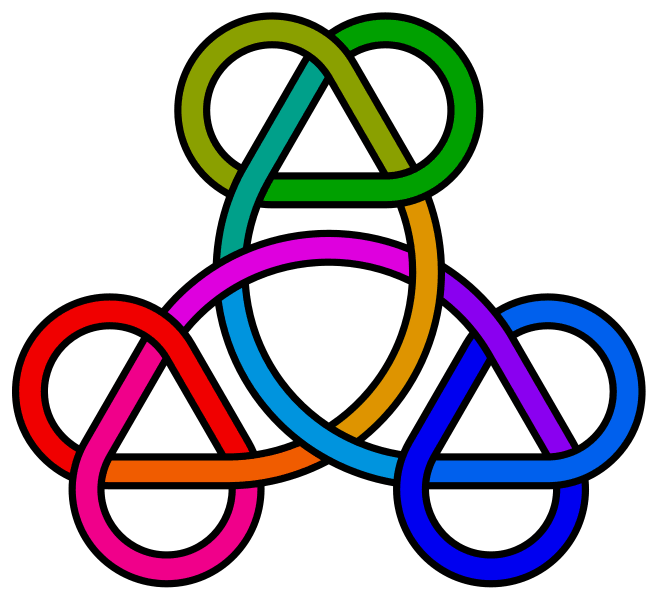3 1 Further Notes and Views: Difference between revisions

From Knot Atlas
Jump to navigationJump to search
No edit summary
No edit summary
Line 107: Line 107:
}}
}}
{{Knot View Template|
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
image = Impossible trefoil knot Isometric.png |
text = Trefoil knot as impossible object|
⚫
text = Banco Do Brasil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html]|
}}
}}
|- valign=top
|- valign=top
Line 122: Line 122:
image = DylansTrefoil_120.jpg |
image = DylansTrefoil_120.jpg |
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
text = Thurston's Trefoil - Figure Eight Trick [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/TrefoilFigureEight/index.html]|
}}
{{Knot View Template|
image = BancoDoBrasil_160.jpg |
⚫
text = Banco Do Brasil [http://www.math.toronto.edu/~drorbn/Gallery/KnottedObjects/BancoDoBrasil.html]|
}}
}}
|}
|}

Revision as of 22:46, 2 June 2011

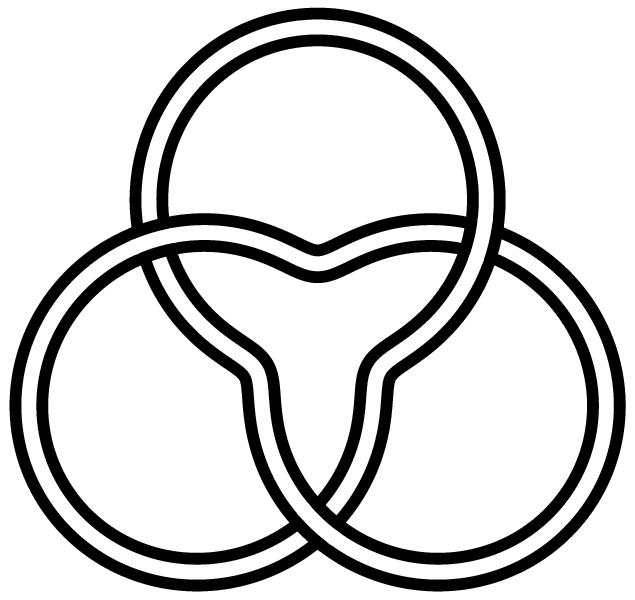
The trefoil is perhaps the easiest knot to find in "nature", and is topologically equivalent to the interlaced form of the common Christian and pagan "triquetra" symbol [12]:

Logo of Caixa Geral de Depositos, Lisboa [1]
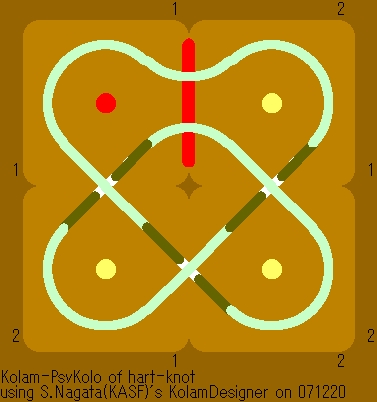A knot consists of two harts in Kolam [2]
A basic form of the interlaced Triquetra; as a Christian symbol, it refers to the Trinity
3D depiction
Further images...
Trefoil/triquetra without outside corners (made from straight lines and 240° circular arcs)
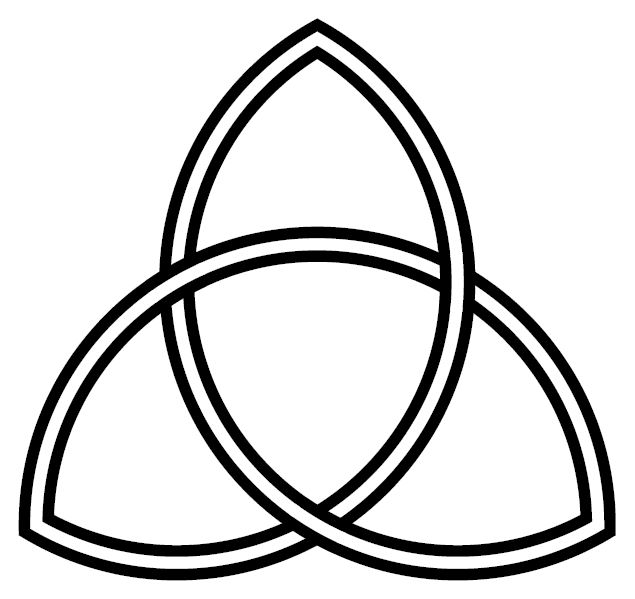Triquetra made from circular arc ribbons
Tightly-knotted form
Celtic-style
A Knotted Box [3]
A trefoil near the Hollander York Gallery [4]
A Knotted Pencil [5]
Trefoil depicted in non-threefold form
3D depiction in non-threefold form
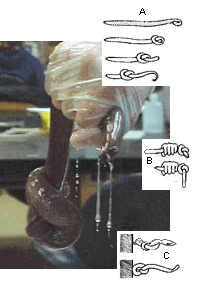A hagfish tying itself in a knot to escape capture. [6]
One version of the Germanic "Valknut" symbol
A Kenyan Stone [7]
Square depiction
In the form of an architectural trefoil
Polar equation curve.
Alternate Valknut depiction
Simple overhand knot of practical knot-tying
Tightly folded pentagonal overhand knot
Visually fancier square trefoil
Trefoil knot as impossible object
The NeverEnding Story logo is a connected sum of two trefoils. [8]
Mike Hutchings' Rope Trick [9]
Thurston's Trefoil - Figure Eight Trick [10]
Banco Do Brasil [11]

Non-prime (compound) versions

  • Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

    Two trefoils (single-closed-loop version of the "granny knot" of practical knot-tying).

  • Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

    Two trefoils (single-closed-loop version of the "square knot" of practical knot-tying)

  • 3D square knot

    3D square knot

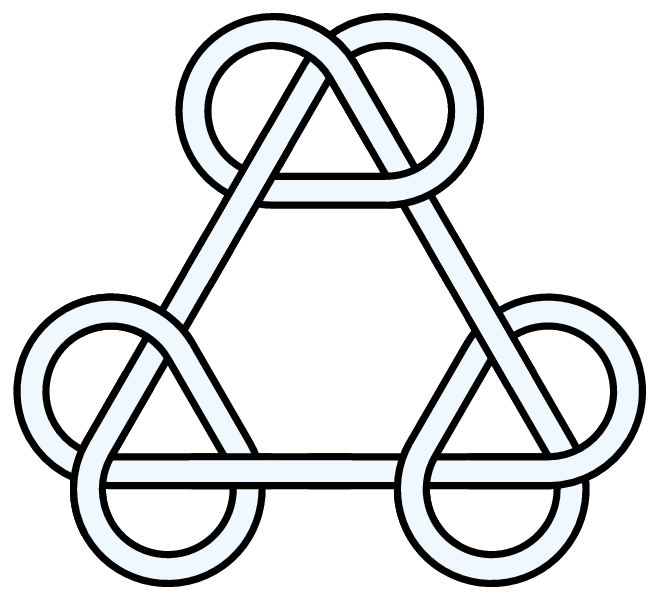
  • Three trefoils (symmetrical).

    Three trefoils (symmetrical).

  • Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

    Four trefoils (Celtic or pseudo-Celtic decorative knot which fits in square)

  • Three trefoils along a closed loop which itself is knotted as a trefoil.

    Three trefoils along a closed loop which itself is knotted as a trefoil.

For configurations of two trefoils along a closed loop which are prime, see 8_15 and 10_120. For a configuration of three trefoils along a closed loop which is prime, see K13a248. For a prime link consisting of two joined trefoils, see L10a108.


Retrieved from "https://katlas.org/index.php?title=3_1_Further_Notes_and_Views&oldid=1712778"