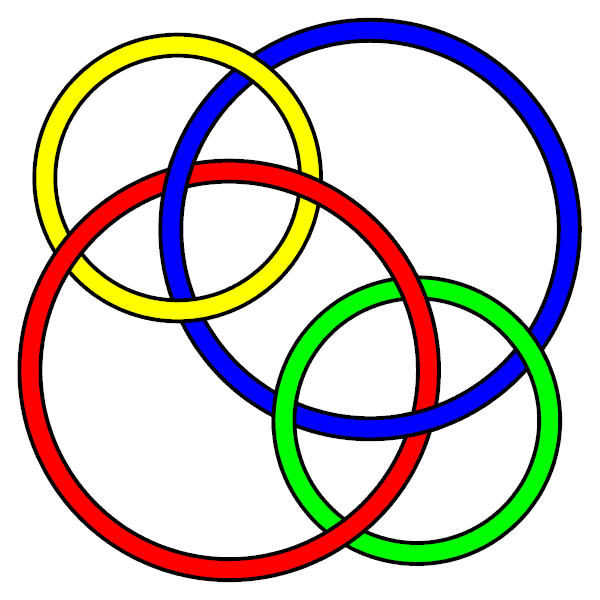User talk:Drorbn

Hello again, Mr. Bar Natan. Thank you for helping me out with my problem. Dr. Conant said that your two examples were similar to his. Anyway, Dr. Conant told me that he became interested in knot theory because you showed up at a presentation he attended. I hope your knot theory career remains a successful one.

Strongbad, 2006-03-14 09:58-05:00

Clarification?

Hi, I just e-mailed you about the "Borromean" bathroom tile, but then realized I could have more easily left a comment here...

Anyway, on the main page, you should probably make it clear that the Rolfsen table is for single-loop knots, while the Thistlewaite table is for multi-loop knots (for people who don't already know that in advance). Thanks. AnonMoos 00:21, 27 Mar 2006 (EST)

P.S., the "Shirt seen in Lisboa" at http://www.math.toronto.edu/~drorbn/Talks/Oporto-0407/KnotsInLisboa.html is actually a partial view of a monochromatic version of the U.S. Bicentennial emblem of 1976. See http://en.wikipedia.org/wiki/Image:Bicentlogo.png

Borromean chain-mail knot?

Which knot number is the "Borromean chain mail" knot? It's not L10a169, but I'm having difficulty determining which it actually is... AnonMoos 15:49, 27 Mar 2006 (EST)

Can't tell without a bit of a search, but I'm running out of time for today... --Drorbn 17:42, 27 Mar 2006 (EST)

Ok, it is L10n107. --Drorbn 21:46, 27 Mar 2006 (EST)

Ok, thanks (of course, I just assumed it was alternating without examining it). AnonMoos 23:40, 28 Mar 2006 (EST)