DT (Dowker-Thistlethwaite) Codes

The DT notation

The "DT Code" ("DT" after Clifford Hugh Dowker and Morwen Thistlethwaite) of a knot $K$ is obtained as follows:

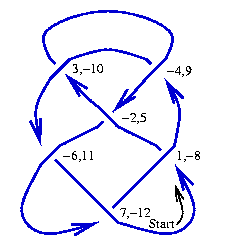
• Start "walking" along </nowiki>$K$ and count every crossing you pass through. If $K$ has $n$ crossings and given that every crossing is visited twice, the count ends at $2n$. Label each crossing with the values of the counter when it is visited, though when labeling by an even number, take it with a minus sign if you are walking "under" the crossing.
• Every crossing is now labeled with two integers whose absolute values run from $1$ to $2n$. It is easy to see that each crossing is labeled with one odd integer and one even integer. The DT code of $K$ is the list of even integers paired with the odd integers 1, 3, 5, ..., taken in this order. See the figure on the right.

KnotTheory` has some rudimentary support for DT codes:

Thus for example, the DT codes for the last 9 crossing alternating knot 9_41 and the first 9 crossing non alternating knot 9_42 are:

(The DT code of an alternating knot is always a sequence of positive numbers but the DT code of a non alternating knot contains both signs.)

DT codes and Gauss codes carry the same information and are easily convertible:

Conversion between DT codes and/or Gauss codes and PD codes is more complicated; the harder side, going from DT/Gauss to PD, was written by Siddarth Sankaran at the University of Toronto: