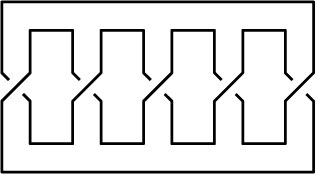
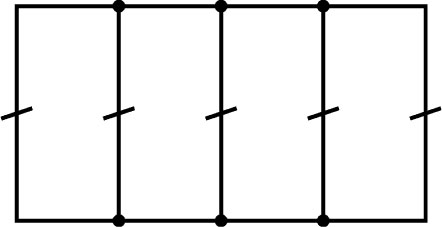
|

|
| 2
|

|
| 3
|

|
| 4
|

|
| 5
|

|
| 6
|

|
| 7
|

|
</nowiki>
{{InOut |
n = 3 |
in = <nowiki>GaussCode[Knot[5, 1]] |
out = GaussCode[-1, 4, -2, 5, -3, 1, -4, 2, -5, 3] }}</nowiki>
{{InOut |
n = 4 |
in = <nowiki>DTCode[Knot[5, 1]] |
out = DTCode[6, 8, 10, 2, 4] }}</nowiki>
{{InOut |
n = 5 |
in = <nowiki>br = BR[Knot[5, 1]] |
out = BR[2, {-1, -1, -1, -1, -1}] }}</nowiki>
{{InOut |
n = 6 |
in = <nowiki>{First[br], Crossings[br]} |
out = {2, 5} }}</nowiki>
{{InOut |
n = 7 |
in = <nowiki>BraidIndex[Knot[5, 1]] |
out = 2 }}</nowiki>
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[8]:=
Show[DrawMorseLink[Knot[5, 1]]]
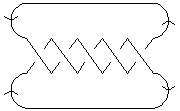 Out[8]=-Graphics-
Out[8]=-Graphics-</nowiki>
{{InOut |
n = 9 |
in = <nowiki> (#[Knot[5, 1]]&) /@ {
SymmetryType, UnknottingNumber, ThreeGenus,
BridgeIndex, SuperBridgeIndex, NakanishiIndex
} |
out = {Reversible, 2, 2, 2, 3, 1} }}</nowiki>
{{InOut |
n = 10 |
in = <nowiki>alex = Alexander[Knot[5, 1]][t] |
out = -2 1 2
1 + t - - - t + t
t }}</nowiki>
{{InOut |
n = 11 |
in = <nowiki>Conway[Knot[5, 1]][z] |
out = 2 4
1 + 3 z + z }}</nowiki>
{{InOut |
n = 12 |
in = <nowiki>Select[AllKnots[], (alex === Alexander[#][t])&] |
out = {Knot[5, 1], Knot[10, 132]} }}</nowiki>
{{InOut |
n = 13 |
in = <nowiki>{KnotDet[Knot[5, 1]], KnotSignature[Knot[5, 1]]} |
out = {5, -4} }}</nowiki>
{{InOut |
n = 14 |
in = <nowiki>Jones[Knot[5, 1]][q] |
out = -7 -6 -5 -4 -2
-q + q - q + q + q }}</nowiki>
{{InOut |
n = 15 |
in = <nowiki>Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&] |
out = {Knot[5, 1], Knot[10, 132]} }}</nowiki>
{{InOut |
n = 16 |
in = <nowiki>A2Invariant[Knot[5, 1]][q] |
out = -22 -20 -18 -14 -12 2 -8 -6
-q - q - q + q + q + --- + q + q
10
q }}</nowiki>
{{InOut |
n = 17 |
in = <nowiki>HOMFLYPT[Knot[5, 1]][a, z] |
out = 4 6 4 2 6 2 4 4
3 a - 2 a + 4 a z - a z + a z }}</nowiki>
{{InOut |
n = 18 |
in = <nowiki>Kauffman[Knot[5, 1]][a, z] |
out = 4 6 5 7 9 4 2 6 2 8 2
3 a + 2 a - 2 a z - a z + a z - 4 a z - 3 a z + a z +
5 3 7 3 4 4 6 4
a z + a z + a z + a z }}</nowiki>
{{InOut |
n = 19 |
in = <nowiki>{Vassiliev[2][Knot[5, 1]], Vassiliev[3][Knot[5, 1]]} |
out = {3, -5} }}</nowiki>
{{InOut |
n = 20 |
in = <nowiki>Kh[Knot[5, 1]][q, t] |
out = -5 -3 1 1 1 1
q + q + ------ + ------ + ------ + -----
15 5 11 4 11 3 7 2
q t q t q t q t }}</nowiki>
{{InOut |
n = 21 |
in = <nowiki>ColouredJones[Knot[5, 1], 2][q] |
out = -19 -18 -16 2 -13 -12 -10 -9 -7 -4
q - q + q - --- + q - q + q - q + q + q
15
q }}</nowiki> }}






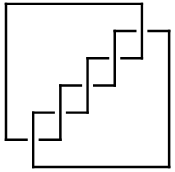


 Out[8]=-Graphics-</nowiki>
Out[8]=-Graphics-</nowiki>