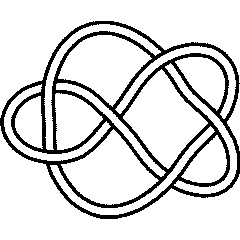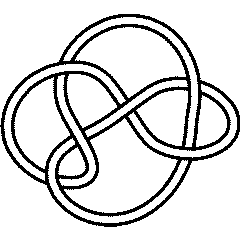6 2

6_1

6_3

Visit 6 2's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 6 2's page at Knotilus! Visit 6 2's page at the original Knot Atlas! Dror likes to call 6_2 "The Miller Institute Knot", as it is the logo of the Miller Institute for Basic Research. The bowline knot of practical knot tying deforms to 6_2.

The Miller Institute Mug [1]

Simple square depiction

3D depiction

Knot presentations

Planar diagram presentation	X1425 X5,10,6,11 X3948 X9,3,10,2 X7,12,8,1 X11,6,12,7
Gauss code	-1, 4, -3, 1, -2, 6, -5, 3, -4, 2, -6, 5
Dowker-Thistlethwaite code	4 8 10 12 2 6
Conway Notation	[312]

Minimum Braid Representative: Length is 6, width is 3. Braid index is 3.

A Morse Link Presentation:

Three dimensional invariants

Symmetry type Reversible Unknotting number 1 3-genus 2 Bridge index 2 Super bridge index $\{3,4\}$ Nakanishi index 1 Maximal Thurston-Bennequin number [-7][-1] Hyperbolic Volume 4.40083 A-Polynomial See Data:6 2/A-polynomial

[edit Notes for 6 2's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus $1$ Topological 4 genus $1$ Concordance genus $2$ Rasmussen s-Invariant -2

[edit Notes for 6 2's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$-t^{2}+3t-3+3t^{-1}-t^{-2}$
Conway polynomial	$-z^{4}-z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 11, -2 }
Jones polynomial	$q-1+2q^{-1}-2q^{-2}+2q^{-3}-2q^{-4}+q^{-5}$
HOMFLY-PT polynomial (db, data sources)	$z^{2}a^{4}+a^{4}-z^{4}a^{2}-3z^{2}a^{2}-2a^{2}+z^{2}+2$
Kauffman polynomial (db, data sources)	$z^{2}a^{6}+2z^{3}a^{5}-za^{5}+2z^{4}a^{4}-2z^{2}a^{4}+a^{4}+z^{5}a^{3}-za^{3}+3z^{4}a^{2}-6z^{2}a^{2}+2a^{2}+z^{5}a-2z^{3}a+z^{4}-3z^{2}+2$
The A2 invariant	$q^{16}-q^{8}-q^{4}+q^{2}+1+q^{-2}+q^{-4}$
The G2 invariant	$q^{86}-q^{84}+q^{82}-q^{80}-q^{78}-q^{74}+3q^{72}-2q^{70}+q^{68}+2q^{62}-q^{60}+q^{58}+q^{56}+q^{52}+3q^{46}-3q^{44}+q^{42}-q^{40}-q^{38}+2q^{36}-4q^{34}+q^{32}-2q^{30}-3q^{24}+q^{22}-q^{20}-q^{14}+q^{12}+q^{10}+2q^{6}-q^{4}+2q^{2}+1-q^{-2}+3q^{-4}-q^{-6}+2q^{-8}-q^{-12}+2q^{-14}+q^{-18}$

Further Quantum Invariants[show]

Further quantum knot invariants for 6_2.

A1 Invariants.

Weight	Invariant
1	$q^{11}-q^{9}+q+q^{-3}$
2	$q^{30}-q^{28}-q^{26}+2q^{24}-q^{22}-q^{20}+q^{18}+q^{10}-q^{6}+q^{4}+q^{2}-1+q^{-2}+q^{-4}-q^{-6}+q^{-10}$
3	$q^{57}-q^{55}-q^{53}+q^{51}+q^{49}-q^{47}-3q^{45}+2q^{43}+3q^{41}-q^{39}-2q^{37}+q^{35}+2q^{33}-q^{29}-q^{27}-2q^{19}-q^{17}+2q^{15}+2q^{13}-q^{11}+2q^{7}+2q^{5}-q^{3}-2q+q^{-1}+2q^{-3}-2q^{-7}+2q^{-11}+q^{-13}-q^{-15}-q^{-17}+q^{-21}$
4	$q^{92}-q^{90}-q^{88}+q^{86}+q^{82}-3q^{80}-q^{78}+3q^{76}+2q^{74}+3q^{72}-5q^{70}-4q^{68}+3q^{66}+4q^{64}+3q^{62}-5q^{60}-5q^{58}+2q^{54}+3q^{52}-q^{50}-2q^{48}+q^{44}+2q^{42}+2q^{40}+q^{38}-2q^{36}-2q^{34}+2q^{30}+q^{28}-3q^{26}-3q^{24}-q^{22}+4q^{20}+2q^{18}-3q^{16}-2q^{14}+5q^{10}+3q^{8}-2q^{6}-2q^{4}-2q^{2}+4+4q^{-2}-2q^{-6}-4q^{-8}+q^{-10}+3q^{-12}+2q^{-14}-4q^{-18}-q^{-20}+q^{-22}+2q^{-24}+2q^{-26}-q^{-28}-q^{-30}-q^{-32}+q^{-36}$
5	$q^{135}-q^{133}-q^{131}+q^{129}-q^{123}-q^{121}+3q^{117}+4q^{115}-5q^{111}-5q^{109}+4q^{105}+8q^{103}+3q^{101}-8q^{99}-10q^{97}-5q^{95}+5q^{93}+11q^{91}+7q^{89}-2q^{87}-9q^{85}-6q^{83}+q^{81}+6q^{79}+6q^{77}+q^{75}-4q^{73}-5q^{71}-2q^{69}+q^{67}+2q^{65}+3q^{63}+q^{61}-q^{59}-2q^{57}-3q^{55}-q^{53}+3q^{51}+4q^{49}+q^{47}-3q^{45}-5q^{43}-q^{41}+5q^{39}+5q^{37}+q^{35}-4q^{33}-6q^{31}-q^{29}+5q^{27}+6q^{25}-6q^{21}-7q^{19}-2q^{17}+7q^{15}+8q^{13}+3q^{11}-4q^{9}-7q^{7}-3q^{5}+3q^{3}+8q+6q^{-1}-q^{-3}-6q^{-5}-6q^{-7}-2q^{-9}+4q^{-11}+7q^{-13}+4q^{-15}-q^{-17}-5q^{-19}-5q^{-21}-q^{-23}+3q^{-25}+5q^{-27}+3q^{-29}-q^{-31}-4q^{-33}-3q^{-35}-q^{-37}+q^{-39}+3q^{-41}+2q^{-43}-q^{-47}-q^{-49}-q^{-51}+q^{-55}$
6	$q^{186}-q^{184}-q^{182}+q^{180}-2q^{174}+q^{172}+5q^{166}+2q^{164}-2q^{162}-6q^{160}-3q^{158}-3q^{156}+3q^{154}+12q^{152}+7q^{150}-3q^{148}-14q^{146}-10q^{144}-8q^{142}+4q^{140}+21q^{138}+17q^{136}+5q^{134}-14q^{132}-18q^{130}-17q^{128}-3q^{126}+18q^{124}+20q^{122}+12q^{120}-5q^{118}-13q^{116}-17q^{114}-9q^{112}+7q^{110}+13q^{108}+12q^{106}+2q^{104}-4q^{102}-10q^{100}-9q^{98}-2q^{96}+3q^{94}+6q^{92}+4q^{90}+3q^{88}-q^{86}-3q^{84}-4q^{82}-3q^{80}+4q^{76}+6q^{74}+4q^{72}-6q^{68}-6q^{66}-3q^{64}+5q^{62}+8q^{60}+5q^{58}-q^{56}-11q^{54}-8q^{52}-q^{50}+8q^{48}+9q^{46}+4q^{44}-4q^{42}-14q^{40}-9q^{38}+q^{36}+12q^{34}+12q^{32}+7q^{30}-4q^{28}-16q^{26}-12q^{24}-q^{22}+12q^{20}+14q^{18}+11q^{16}-15q^{12}-15q^{10}-7q^{8}+7q^{6}+12q^{4}+15q^{2}+7-8q^{-2}-13q^{-4}-12q^{-6}-2q^{-8}+4q^{-10}+14q^{-12}+13q^{-14}+2q^{-16}-5q^{-18}-11q^{-20}-9q^{-22}-6q^{-24}+5q^{-26}+10q^{-28}+8q^{-30}+4q^{-32}-2q^{-34}-6q^{-36}-10q^{-38}-3q^{-40}+2q^{-42}+5q^{-44}+6q^{-46}+4q^{-48}+q^{-50}-5q^{-52}-4q^{-54}-3q^{-56}-q^{-58}+q^{-60}+3q^{-62}+3q^{-64}-q^{-70}-q^{-72}-q^{-74}+q^{-78}$

A2 Invariants.

Weight	Invariant
1,0	$q^{16}-q^{8}-q^{4}+q^{2}+1+q^{-2}+q^{-4}$
1,1	$q^{44}-2q^{42}+2q^{40}-2q^{38}+5q^{36}-4q^{34}+2q^{32}-4q^{30}-2q^{24}+6q^{22}-4q^{20}+8q^{18}-6q^{16}+6q^{14}-6q^{12}+4q^{10}-2q^{8}+q^{4}-2q^{2}+4-4q^{-2}+4q^{-4}-2q^{-6}+4q^{-8}+q^{-12}$
2,0	$q^{40}-q^{30}-2q^{28}+q^{20}+2q^{18}+q^{16}+q^{14}+q^{12}-q^{8}-q^{6}-q^{2}+q^{-2}+q^{-4}+q^{-8}+q^{-10}+q^{-12}$
3,0	$q^{72}-3q^{60}-2q^{58}-q^{56}+2q^{54}+2q^{52}+2q^{46}+4q^{44}+2q^{42}-q^{38}-q^{34}-3q^{32}-4q^{30}-3q^{28}-2q^{26}-q^{24}-q^{22}+2q^{20}+4q^{18}+4q^{16}+3q^{14}+2q^{12}+3q^{10}+q^{8}-q^{6}-3q^{4}-q^{2}+1+q^{-2}-q^{-4}-q^{-6}+2q^{-10}+q^{-12}-q^{-16}+q^{-20}+q^{-22}+q^{-24}$

A3 Invariants.

Weight	Invariant
0,1,0	$q^{36}-q^{34}-q^{32}+q^{30}-q^{28}+2q^{24}+q^{22}+q^{20}+q^{18}-q^{14}-2q^{12}-q^{10}-q^{8}-2q^{6}+q^{4}+2q^{2}+1+2q^{-2}+2q^{-4}+q^{-8}$
1,0,0	$q^{21}+q^{17}-q^{11}-q^{9}-q^{7}-q^{5}+q^{3}+q+2q^{-1}+q^{-3}+q^{-5}$
1,0,1	$q^{58}-2q^{56}+q^{54}+q^{52}-2q^{50}+5q^{48}-2q^{46}-q^{44}+2q^{42}-5q^{40}+3q^{38}-2q^{36}-2q^{34}+3q^{32}-5q^{30}+2q^{28}+q^{26}+4q^{22}+4q^{20}+q^{18}+3q^{16}+2q^{14}-4q^{12}+3q^{10}-7q^{8}-q^{6}-q^{4}-5q^{2}+4-2q^{-2}+5q^{-4}+4q^{-6}+2q^{-8}+4q^{-10}+q^{-14}$

A4 Invariants.

Weight	Invariant
0,1,0,0	$q^{46}-q^{42}-q^{36}-q^{34}+q^{32}+q^{30}+q^{28}+2q^{26}+3q^{24}+q^{22}+q^{18}-2q^{16}-3q^{14}-2q^{12}-2q^{10}-3q^{8}-q^{6}+q^{4}+2q^{2}+2+3q^{-2}+3q^{-4}+2q^{-6}+q^{-8}+q^{-10}$
1,0,0,0	$q^{26}+q^{22}+q^{20}-q^{14}-q^{12}-2q^{10}-q^{8}-q^{6}+q^{4}+q^{2}+2+2q^{-2}+q^{-4}+q^{-6}$

B2 Invariants.

Weight	Invariant
0,1	$q^{36}-q^{34}+q^{32}-q^{30}+q^{28}+q^{22}-q^{20}+q^{18}-2q^{16}+q^{14}-2q^{12}+q^{10}-q^{8}+q^{4}+1+2q^{-4}+q^{-8}$
1,0	$q^{58}-q^{54}-q^{52}+q^{48}-q^{44}+q^{40}+q^{38}+q^{32}+q^{30}-q^{26}-q^{18}-q^{16}-q^{10}-q^{8}+q^{6}+q^{4}+q^{2}+q^{-4}+2q^{-6}+q^{-14}$

D4 Invariants.

Weight	Invariant
1,0,0,0	$q^{50}-q^{48}-q^{44}+q^{42}-q^{40}+q^{34}+2q^{32}+q^{30}+2q^{28}+2q^{24}-q^{22}-3q^{18}-q^{16}-3q^{14}-q^{12}-2q^{10}-q^{8}+q^{6}+q^{4}+2q^{2}+2+3q^{-2}+q^{-4}+2q^{-6}+q^{-10}$

G2 Invariants.

Weight	Invariant
1,0	$q^{86}-q^{84}+q^{82}-q^{80}-q^{78}-q^{74}+3q^{72}-2q^{70}+q^{68}+2q^{62}-q^{60}+q^{58}+q^{56}+q^{52}+3q^{46}-3q^{44}+q^{42}-q^{40}-q^{38}+2q^{36}-4q^{34}+q^{32}-2q^{30}-3q^{24}+q^{22}-q^{20}-q^{14}+q^{12}+q^{10}+2q^{6}-q^{4}+2q^{2}+1-q^{-2}+3q^{-4}-q^{-6}+2q^{-8}-q^{-12}+2q^{-14}+q^{-18}$

.

Computer Talk[show]

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["6 2"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$-t^{2}+3t-3+3t^{-1}-t^{-2}$

In[5]:=

Conway[K][z]

Out[5]=

$-z^{4}-z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 11, -2 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$q-1+2q^{-1}-2q^{-2}+2q^{-3}-2q^{-4}+q^{-5}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$z^{2}a^{4}+a^{4}-z^{4}a^{2}-3z^{2}a^{2}-2a^{2}+z^{2}+2$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$z^{2}a^{6}+2z^{3}a^{5}-za^{5}+2z^{4}a^{4}-2z^{2}a^{4}+a^{4}+z^{5}a^{3}-za^{3}+3z^{4}a^{2}-6z^{2}a^{2}+2a^{2}+z^{5}a-2z^{3}a+z^{4}-3z^{2}+2$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {...}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {...}

Vassiliev invariants

V2 and V3:

(-1, 1)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $-4$ $8$ $8$ ${\frac {34}{3}}$ ${\frac {38}{3}}$ $-32$ $-{\frac {208}{3}}$ $-{\frac {64}{3}}$ $-24$ $-{\frac {32}{3}}$ $32$ $-{\frac {136}{3}}$ $-{\frac {152}{3}}$ ${\frac {2129}{30}}$ ${\frac {662}{15}}$ $-{\frac {1862}{45}}$ ${\frac {463}{18}}$ $-{\frac {751}{30}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$-2 is the signature of 6 2. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ -4 -3 -2 -1 0 1 2 χ 3             1 1 1               0 -1         2 1   1 -3       1 1     0 -5     1 1       0 -7   1 1         0 -9   1           -1 -11 1             1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=-3$ $i=-1$ $r=-4$ ${\mathbb {Z} }$ $r=-3$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-2$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=-1$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=0$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }^{2}$ $r=1$ ${\mathbb {Z} }$ $r=2$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the $n+1$-dimensional representation of $sl(2)$)[show]

$n$	$J_{n}$
2	$q^{4}-q^{3}-q^{2}+3q-1-3q^{-1}+5q^{-2}-q^{-3}-5q^{-4}+6q^{-5}-6q^{-7}+6q^{-8}-5q^{-10}+4q^{-11}-2q^{-13}+q^{-14}$
3	$q^{9}-q^{8}-q^{7}+3q^{5}-3q^{3}-2q^{2}+5q+2-4q^{-1}-5q^{-2}+6q^{-3}+5q^{-4}-4q^{-5}-7q^{-6}+5q^{-7}+8q^{-8}-4q^{-9}-10q^{-10}+4q^{-11}+10q^{-12}-4q^{-13}-10q^{-14}+3q^{-15}+10q^{-16}-3q^{-17}-8q^{-18}+2q^{-19}+7q^{-20}-2q^{-21}-4q^{-22}+q^{-23}+2q^{-24}-2q^{-26}+q^{-27}$
4	$q^{16}-q^{15}-q^{14}+4q^{11}-q^{10}-2q^{9}-2q^{8}-3q^{7}+8q^{6}+q^{5}-q^{4}-4q^{3}-8q^{2}+10q+3+3q^{-1}-4q^{-2}-14q^{-3}+10q^{-4}+3q^{-5}+8q^{-6}-2q^{-7}-19q^{-8}+8q^{-9}+2q^{-10}+13q^{-11}-24q^{-13}+6q^{-14}+2q^{-15}+17q^{-16}+q^{-17}-26q^{-18}+4q^{-19}+2q^{-20}+20q^{-21}+2q^{-22}-26q^{-23}+3q^{-24}+q^{-25}+18q^{-26}+3q^{-27}-22q^{-28}+2q^{-29}-q^{-30}+13q^{-31}+3q^{-32}-14q^{-33}+3q^{-34}-2q^{-35}+6q^{-36}+2q^{-37}-6q^{-38}+2q^{-39}-q^{-40}+2q^{-41}-2q^{-43}+q^{-44}$
5	$q^{25}-q^{24}-q^{23}+q^{20}+3q^{19}-3q^{17}-2q^{16}-2q^{15}+6q^{13}+4q^{12}-q^{11}-4q^{10}-6q^{9}-4q^{8}+6q^{7}+8q^{6}+4q^{5}-q^{4}-9q^{3}-10q^{2}+2q+8+9q^{-1}+6q^{-2}-7q^{-3}-15q^{-4}-4q^{-5}+4q^{-6}+12q^{-7}+13q^{-8}-2q^{-9}-16q^{-10}-13q^{-11}-q^{-12}+13q^{-13}+19q^{-14}+4q^{-15}-17q^{-16}-19q^{-17}-6q^{-18}+15q^{-19}+24q^{-20}+8q^{-21}-17q^{-22}-25q^{-23}-10q^{-24}+17q^{-25}+28q^{-26}+11q^{-27}-18q^{-28}-29q^{-29}-12q^{-30}+18q^{-31}+29q^{-32}+13q^{-33}-16q^{-34}-30q^{-35}-13q^{-36}+15q^{-37}+26q^{-38}+14q^{-39}-11q^{-40}-25q^{-41}-13q^{-42}+10q^{-43}+19q^{-44}+11q^{-45}-4q^{-46}-16q^{-47}-9q^{-48}+4q^{-49}+9q^{-50}+6q^{-51}-2q^{-52}-5q^{-53}-4q^{-54}+5q^{-56}+q^{-57}-2q^{-58}-q^{-61}+2q^{-62}-2q^{-64}+q^{-65}$
6	$q^{36}-q^{35}-q^{34}+q^{31}+4q^{29}-q^{28}-3q^{27}-2q^{26}-2q^{25}-q^{23}+10q^{22}+2q^{21}-q^{20}-3q^{19}-5q^{18}-5q^{17}-8q^{16}+14q^{15}+6q^{14}+5q^{13}+q^{12}-3q^{11}-10q^{10}-19q^{9}+11q^{8}+4q^{7}+11q^{6}+8q^{5}+8q^{4}-9q^{3}-29q^{2}+5q-6+10q^{-1}+13q^{-2}+23q^{-3}-q^{-4}-32q^{-5}-20q^{-7}+2q^{-8}+13q^{-9}+38q^{-10}+10q^{-11}-29q^{-12}-2q^{-13}-33q^{-14}-9q^{-15}+9q^{-16}+50q^{-17}+21q^{-18}-24q^{-19}-2q^{-20}-44q^{-21}-19q^{-22}+4q^{-23}+60q^{-24}+29q^{-25}-19q^{-26}-3q^{-27}-53q^{-28}-26q^{-29}+q^{-30}+70q^{-31}+35q^{-32}-16q^{-33}-6q^{-34}-61q^{-35}-29q^{-36}+q^{-37}+76q^{-38}+39q^{-39}-14q^{-40}-8q^{-41}-65q^{-42}-32q^{-43}+77q^{-45}+41q^{-46}-10q^{-47}-7q^{-48}-63q^{-49}-35q^{-50}-5q^{-51}+70q^{-52}+40q^{-53}-4q^{-54}-q^{-55}-53q^{-56}-34q^{-57}-11q^{-58}+54q^{-59}+32q^{-60}+7q^{-62}-36q^{-63}-26q^{-64}-13q^{-65}+33q^{-66}+18q^{-67}-q^{-68}+11q^{-69}-17q^{-70}-14q^{-71}-9q^{-72}+16q^{-73}+6q^{-74}-3q^{-75}+7q^{-76}-6q^{-77}-4q^{-78}-4q^{-79}+7q^{-80}-3q^{-82}+4q^{-83}-2q^{-84}-q^{-86}+2q^{-87}-2q^{-89}+q^{-90}$
7	$q^{49}-q^{48}-q^{47}+q^{44}+q^{42}+3q^{41}-q^{40}-3q^{39}-2q^{38}-3q^{37}+q^{36}+q^{34}+9q^{33}+3q^{32}-q^{31}-3q^{30}-8q^{29}-3q^{28}-5q^{27}-4q^{26}+12q^{25}+9q^{24}+7q^{23}+5q^{22}-9q^{21}-5q^{20}-12q^{19}-16q^{18}+6q^{17}+7q^{16}+13q^{15}+18q^{14}+q^{13}+3q^{12}-12q^{11}-28q^{10}-6q^{9}-7q^{8}+6q^{7}+25q^{6}+14q^{5}+21q^{4}-29q^{2}-14q-25-15q^{-1}+19q^{-2}+19q^{-3}+40q^{-4}+22q^{-5}-18q^{-6}-11q^{-7}-41q^{-8}-38q^{-9}+2q^{-10}+12q^{-11}+51q^{-12}+46q^{-13}+q^{-14}-q^{-15}-48q^{-16}-59q^{-17}-17q^{-18}-4q^{-19}+55q^{-20}+67q^{-21}+20q^{-22}+14q^{-23}-51q^{-24}-75q^{-25}-36q^{-26}-19q^{-27}+55q^{-28}+82q^{-29}+38q^{-30}+27q^{-31}-52q^{-32}-90q^{-33}-49q^{-34}-30q^{-35}+57q^{-36}+95q^{-37}+52q^{-38}+34q^{-39}-56q^{-40}-102q^{-41}-58q^{-42}-34q^{-43}+60q^{-44}+106q^{-45}+61q^{-46}+35q^{-47}-61q^{-48}-112q^{-49}-63q^{-50}-36q^{-51}+63q^{-52}+114q^{-53}+66q^{-54}+36q^{-55}-63q^{-56}-115q^{-57}-68q^{-58}-40q^{-59}+61q^{-60}+116q^{-61}+71q^{-62}+41q^{-63}-57q^{-64}-111q^{-65}-71q^{-66}-47q^{-67}+49q^{-68}+107q^{-69}+72q^{-70}+49q^{-71}-43q^{-72}-94q^{-73}-66q^{-74}-52q^{-75}+28q^{-76}+83q^{-77}+63q^{-78}+50q^{-79}-23q^{-80}-67q^{-81}-47q^{-82}-47q^{-83}+9q^{-84}+51q^{-85}+39q^{-86}+41q^{-87}-8q^{-88}-35q^{-89}-24q^{-90}-31q^{-91}+2q^{-92}+22q^{-93}+14q^{-94}+23q^{-95}+q^{-96}-16q^{-97}-8q^{-98}-13q^{-99}+3q^{-100}+7q^{-101}-q^{-102}+10q^{-103}+2q^{-104}-6q^{-105}-2q^{-106}-4q^{-107}+3q^{-108}+2q^{-109}-4q^{-110}+3q^{-111}+2q^{-112}-2q^{-113}-q^{-115}+2q^{-116}-2q^{-118}+q^{-119}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 29, 2005, 15:27:48)...
In[2]:=	PD[Knot[6, 2]]
Out[2]=	PD[X[1, 4, 2, 5], X[5, 10, 6, 11], X[3, 9, 4, 8], X[9, 3, 10, 2], X[7, 12, 8, 1], X[11, 6, 12, 7]]
In[3]:=	GaussCode[Knot[6, 2]]
Out[3]=	GaussCode[-1, 4, -3, 1, -2, 6, -5, 3, -4, 2, -6, 5]
In[4]:=	DTCode[Knot[6, 2]]
Out[4]=	DTCode[4, 8, 10, 12, 2, 6]
In[5]:=	br = BR[Knot[6, 2]]
Out[5]=	BR[3, {-1, -1, -1, 2, -1, 2}]
In[6]:=	{First[br], Crossings[br]}
Out[6]=	{3, 6}
In[7]:=	BraidIndex[Knot[6, 2]]
Out[7]=	3
In[8]:=	Show[DrawMorseLink[Knot[6, 2]]]
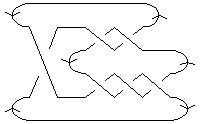Out[8]=	-Graphics-
In[9]:=	(#[Knot[6, 2]]&) /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}
Out[9]=	{Reversible, 1, 2, 2, {3, 4}, 1}
In[10]:=	alex = Alexander[Knot[6, 2]][t]
Out[10]=	-2 3 2 -3 - t + - + 3 t - t t
In[11]:=	Conway[Knot[6, 2]][z]
Out[11]=	2 4 1 - z - z
In[12]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[12]=	{Knot[6, 2]}
In[13]:=	{KnotDet[Knot[6, 2]], KnotSignature[Knot[6, 2]]}
Out[13]=	{11, -2}
In[14]:=	Jones[Knot[6, 2]][q]
Out[14]=	-5 2 2 2 2 -1 + q - -- + -- - -- + - + q 4 3 2 q q q q
In[15]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[15]=	{Knot[6, 2]}
In[16]:=	A2Invariant[Knot[6, 2]][q]
Out[16]=	-16 -8 -4 -2 2 4 1 + q - q - q + q + q + q
In[17]:=	HOMFLYPT[Knot[6, 2]][a, z]
Out[17]=	2 4 2 2 2 4 2 2 4 2 - 2 a + a + z - 3 a z + a z - a z
In[18]:=	Kauffman[Knot[6, 2]][a, z]
Out[18]=	2 4 3 5 2 2 2 4 2 6 2 2 + 2 a + a - a z - a z - 3 z - 6 a z - 2 a z + a z - 3 5 3 4 2 4 4 4 5 3 5 2 a z + 2 a z + z + 3 a z + 2 a z + a z + a z
In[19]:=	{Vassiliev[2][Knot[6, 2]], Vassiliev[3][Knot[6, 2]]}
Out[19]=	{-1, 1}
In[20]:=	Kh[Knot[6, 2]][q, t]
Out[20]=	-3 2 1 1 1 1 1 1 1 t q + - + ------ + ----- + ----- + ----- + ----- + ---- + ---- + - + q 11 4 9 3 7 3 7 2 5 2 5 3 q q t q t q t q t q t q t q t 3 2 q t
In[21]:=	ColouredJones[Knot[6, 2], 2][q]
Out[21]=	-14 2 4 5 6 6 6 5 -3 5 3 -1 + q - --- + --- - --- + -- - -- + -- - -- - q + -- - - + 3 q - 13 11 10 8 7 5 4 2 q q q q q q q q q 2 3 4 q - q + q

See/edit the Rolfsen_Splice_Template.