L11a289

L11a288

L11a290

(Knotscape image)	See the full Thistlethwaite Link Table (up to 11 crossings). Visit L11a289 at Knotilus!

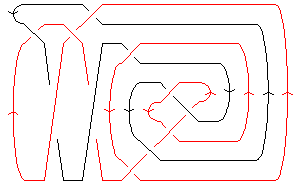
Celtic or pseudo-Celtic linear decorative knot

Decorative variant with big loops at ends

(Also see Detecting a Link Using the Multivariable Alexander Polynomial.)

Link Presentations

[edit Notes on L11a289's Link Presentations]

Planar diagram presentation	X10,1,11,2 X12,4,13,3 X22,12,9,11 X2,9,3,10 X20,14,21,13 X14,7,15,8 X18,16,19,15 X16,6,17,5 X6,18,7,17 X4,19,5,20 X8,22,1,21
Gauss code	{1, -4, 2, -10, 8, -9, 6, -11}, {4, -1, 3, -2, 5, -6, 7, -8, 9, -7, 10, -5, 11, -3}

A Braid Representative
A Morse Link Presentation

Polynomial invariants

Multivariable Alexander Polynomial (in [math]\displaystyle{ u }[/math], [math]\displaystyle{ v }[/math], [math]\displaystyle{ w }[/math], ...)	[math]\displaystyle{ \frac{(u-1) (v-1) \left(u^2 v^2-2 u^2 v+u^2-2 u v^2+2 u v-2 u+v^2-2 v+1\right)}{u^{3/2} v^{3/2}} }[/math] (db)
Jones polynomial	[math]\displaystyle{ 16 q^{9/2}-18 q^{7/2}+17 q^{5/2}-\frac{1}{q^{5/2}}-15 q^{3/2}+\frac{3}{q^{3/2}}+q^{17/2}-4 q^{15/2}+8 q^{13/2}-12 q^{11/2}+10 \sqrt{q}-\frac{7}{\sqrt{q}} }[/math] (db)
Signature	3 (db)
HOMFLY-PT polynomial	[math]\displaystyle{ z^3 a^{-7} +z a^{-7} -2 z^5 a^{-5} -5 z^3 a^{-5} -3 z a^{-5} +z^7 a^{-3} +4 z^5 a^{-3} +7 z^3 a^{-3} +5 z a^{-3} -2 z^5 a^{-1} +a z^3-6 z^3 a^{-1} +2 a z-5 z a^{-1} +a z^{-1} - a^{-1} z^{-1} }[/math] (db)
Kauffman polynomial	[math]\displaystyle{ z^4 a^{-10} +4 z^5 a^{-9} -2 z^3 a^{-9} +8 z^6 a^{-8} -8 z^4 a^{-8} +3 z^2 a^{-8} +10 z^7 a^{-7} -12 z^5 a^{-7} +6 z^3 a^{-7} -2 z a^{-7} +8 z^8 a^{-6} -4 z^6 a^{-6} -9 z^4 a^{-6} +4 z^2 a^{-6} +4 z^9 a^{-5} +9 z^7 a^{-5} -34 z^5 a^{-5} +24 z^3 a^{-5} -6 z a^{-5} +z^{10} a^{-4} +13 z^8 a^{-4} -33 z^6 a^{-4} +16 z^4 a^{-4} +7 z^9 a^{-3} -7 z^7 a^{-3} -24 z^5 a^{-3} +32 z^3 a^{-3} -10 z a^{-3} +z^{10} a^{-2} +8 z^8 a^{-2} -32 z^6 a^{-2} +28 z^4 a^{-2} -4 z^2 a^{-2} +3 z^9 a^{-1} +a z^7-5 z^7 a^{-1} -4 a z^5-10 z^5 a^{-1} +6 a z^3+22 z^3 a^{-1} -4 a z-10 z a^{-1} +a z^{-1} + a^{-1} z^{-1} +3 z^8-11 z^6+12 z^4-3 z^2-1 }[/math] (db)

Khovanov Homology

The coefficients of the monomials [math]\displaystyle{ t^rq^j }[/math] are shown, along with their alternating sums [math]\displaystyle{ \chi }[/math] (fixed [math]\displaystyle{ j }[/math], alternation over [math]\displaystyle{ r }[/math]).

\   r    \    j   \ -4 -3 -2 -1 0 1 2 3 4 5 6 7 χ 18                       1 -1 16                     3   3 14                   5 1   -4 12                 7 3     4 10               9 5       -4 8             9 7         2 6           8 9           1 4         7 9             -2 2       5 10               5 0     2 5                 -3 -2   1 5                   4 -4   2                     -2 -6 1                       1

Integral Khovanov Homology (db, data source)

[math]\displaystyle{ \dim{\mathcal G}_{2r+i}\operatorname{KH}^r_{\mathbb Z} }[/math] [math]\displaystyle{ i=2 }[/math] [math]\displaystyle{ i=4 }[/math] [math]\displaystyle{ r=-4 }[/math] [math]\displaystyle{ {\mathbb Z} }[/math] [math]\displaystyle{ r=-3 }[/math] [math]\displaystyle{ {\mathbb Z}^{2}\oplus{\mathbb Z}_2 }[/math] [math]\displaystyle{ {\mathbb Z} }[/math] [math]\displaystyle{ r=-2 }[/math] [math]\displaystyle{ {\mathbb Z}^{5}\oplus{\mathbb Z}_2^{2} }[/math] [math]\displaystyle{ {\mathbb Z}^{2} }[/math] [math]\displaystyle{ r=-1 }[/math] [math]\displaystyle{ {\mathbb Z}^{5}\oplus{\mathbb Z}_2^{5} }[/math] [math]\displaystyle{ {\mathbb Z}^{5} }[/math] [math]\displaystyle{ r=0 }[/math] [math]\displaystyle{ {\mathbb Z}^{10}\oplus{\mathbb Z}_2^{5} }[/math] [math]\displaystyle{ {\mathbb Z}^{7} }[/math] [math]\displaystyle{ r=1 }[/math] [math]\displaystyle{ {\mathbb Z}^{9}\oplus{\mathbb Z}_2^{8} }[/math] [math]\displaystyle{ {\mathbb Z}^{8} }[/math] [math]\displaystyle{ r=2 }[/math] [math]\displaystyle{ {\mathbb Z}^{9}\oplus{\mathbb Z}_2^{9} }[/math] [math]\displaystyle{ {\mathbb Z}^{9} }[/math] [math]\displaystyle{ r=3 }[/math] [math]\displaystyle{ {\mathbb Z}^{7}\oplus{\mathbb Z}_2^{9} }[/math] [math]\displaystyle{ {\mathbb Z}^{9} }[/math] [math]\displaystyle{ r=4 }[/math] [math]\displaystyle{ {\mathbb Z}^{5}\oplus{\mathbb Z}_2^{7} }[/math] [math]\displaystyle{ {\mathbb Z}^{7} }[/math] [math]\displaystyle{ r=5 }[/math] [math]\displaystyle{ {\mathbb Z}^{3}\oplus{\mathbb Z}_2^{5} }[/math] [math]\displaystyle{ {\mathbb Z}^{5} }[/math] [math]\displaystyle{ r=6 }[/math] [math]\displaystyle{ {\mathbb Z}\oplus{\mathbb Z}_2^{3} }[/math] [math]\displaystyle{ {\mathbb Z}^{3} }[/math] [math]\displaystyle{ r=7 }[/math] [math]\displaystyle{ {\mathbb Z}_2 }[/math] [math]\displaystyle{ {\mathbb Z} }[/math]

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L11a288 L11a290