Arc Presentations: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
An ''Arc Presentation'' <math>A</math> of a knot <math>K</math> (in "grid form", to be precise) is a planar (toroidal, to be precise) picture of the knot in which all arcs are either horizontal or vertical, in which the vertical arcs are alway "above" the horizontal arcs, and in which no two horizontal arcs have the same <math>y</math>-coordinate and no two vertical arcs have the same <math>x</math>-coordinate (read more at [http://www.indiana.edu/~knotinfo/descriptions/arc_index.html]). Without loss of generality, the <math>x</math>-coordinates of the vertical arcs in <math>A</math> are the integers <math>1</math> through <math>n</math> for some <math>n</math>, and the <math>y</math>-coordinates of the horizontal arcs in <math>A</math> are (also!) the integers <math>1</math> through <math>n</math>. |
An ''Arc Presentation'' <math>A</math> of a knot <math>K</math> (in "grid form", to be precise) is a planar (toroidal, to be precise) picture of the knot in which all arcs are either horizontal or vertical, in which the vertical arcs are alway "above" the horizontal arcs, and in which no two horizontal arcs have the same <math>y</math>-coordinate and no two vertical arcs have the same <math>x</math>-coordinate (read more at [http://www.indiana.edu/~knotinfo/descriptions/arc_index.html]). Without loss of generality, the <math>x</math>-coordinates of the vertical arcs in <math>A</math> are the integers <math>1</math> through <math>n</math> for some <math>n</math>, and the <math>y</math>-coordinates of the horizontal arcs in <math>A</math> are (also!) the integers <math>1</math> through <math>n</math>. |
||
[[Image:3 1 AP.gif|thumb|left| |
[[Image:3 1 AP.gif|thumb|left|100px|((5,2), (1,3), (2,4), (3,5), (4,1))]] |
||
Thus for example, on the left is an arc presentation <math>A</math> of the [[3_1|trefoil]] knot. It can be represented numerically by the sequence of ordered pairs shown below it. This sequence reads: the lowest horizontal arc in <math>A</math> connects the 5th vertical arc with the 2nd; the next horizontal arc in <math>A</math> connects the 1st vertical with the 3rd, and so on. In general, an arc presentation involving <math>n</math> horizontal and <math>n</math> vertical arcs will be described in this way by a sequence of <math>n</math> ordered pairs of integers in the range between <math>1</math> and <math>n</math>. |
|||
Thus for example, on the left is an arc presentation of the [[3_1|trefoil]] knot. It can be represented numerically |
|||
Arc presentations are used extensively in the computation of [[Heegaard Floer Knot Homology|Heegaard Floer Knot Homologies]]. |
|||
<br clear=left/> |
|||
<code>KnotTheory`</code> knows about arc presentations: |
<code>KnotTheory`</code> knows about arc presentations: |
||
Revision as of 21:02, 4 December 2007
An Arc Presentation of a knot (in "grid form", to be precise) is a planar (toroidal, to be precise) picture of the knot in which all arcs are either horizontal or vertical, in which the vertical arcs are alway "above" the horizontal arcs, and in which no two horizontal arcs have the same -coordinate and no two vertical arcs have the same -coordinate (read more at [1]). Without loss of generality, the -coordinates of the vertical arcs in are the integers through for some , and the -coordinates of the horizontal arcs in are (also!) the integers through .
Thus for example, on the left is an arc presentation of the trefoil knot. It can be represented numerically by the sequence of ordered pairs shown below it. This sequence reads: the lowest horizontal arc in connects the 5th vertical arc with the 2nd; the next horizontal arc in connects the 1st vertical with the 3rd, and so on. In general, an arc presentation involving horizontal and vertical arcs will be described in this way by a sequence of ordered pairs of integers in the range between and .
Arc presentations are used extensively in the computation of Heegaard Floer Knot Homologies.
KnotTheory` knows about arc presentations:
(For In[1] see Setup)
| ||||
In[2]:=
|
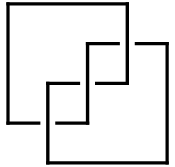
ap = ArcPresentation["K11n11"]
|
Out[2]=
|
ArcPresentation[{12, 2}, {1, 10}, {3, 9}, {5, 11}, {9, 12}, {4, 8},
{2, 5}, {11, 7}, {8, 6}, {7, 4}, {10, 3}, {6, 1}]
|
In[4]:=
|
Draw[ap]
|
| |
Out[4]=
|
-Graphics-
|
In[5]:=
|
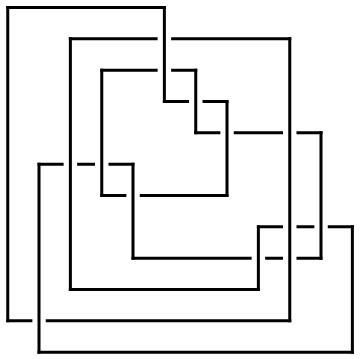
ap0 = ArcPresentation["K11n11", Reduce -> 0]
|
Out[5]=
|
ArcPresentation[{13, 19}, {20, 23}, {19, 22}, {15, 14}, {14, 2},
{1, 13}, {3, 12}, {2, 4}, {16, 18}, {17, 15}, {8, 16}, {12, 17},
{5, 7}, {4, 6}, {7, 11}, {6, 8}, {18, 10}, {11, 9}, {10, 21},
{9, 20}, {21, 5}, {22, 3}, {23, 1}]
|
| ||||
In[8]:=
|
Draw[ap0]
|
| |
Out[8]=
|
-Graphics-
|
In[9]:=
|
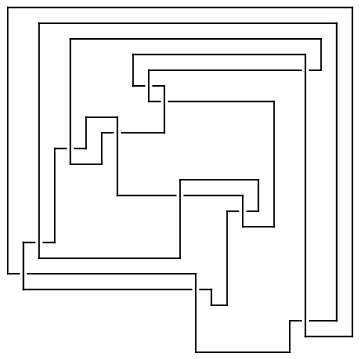
Reflect[ap_ArcPresentation] := ArcPresentation @@ (
(Last /@ Sort[Reverse /@ Position[ap, #]]) & /@ Range[Length[ap]]
)
|
In[11]:=
|
Reflect[ap] // Draw
|
| |
Out[11]=
|
-Graphics-
|
In[12]:=
|
MinesweeperMatrix[ap_ArcPresentation] := Module[
{l, CurrentRow, c1, c2, k, s},
l = Length[ap];
CurrentRow = Table[0, {l}];
Table[
{c1, c2} = Sort[ap[[k]]];
s = Sign[{-1, 1}.ap[[k]]];
Do[
CurrentRow[[c]] += s,
{c, c1, c2 - 1}
];
CurrentRow,
{k, l}
]
];
|
In[14]:=
|
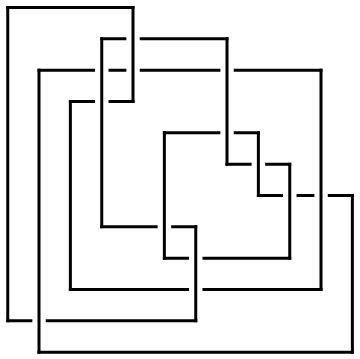
Draw[ap, OverlayMatrix -> MinesweeperMatrix[ap]]
|
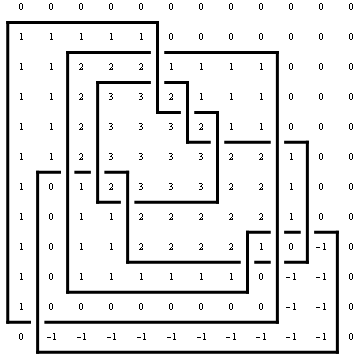
| |
Out[14]=
|
-Graphics-
|
In[15]:=
|
{Det[t^MinesweeperMatrix[ap]], Alexander[ap][t]} // Factor
|
Out[15]=
|
11 2 2 3 4 5 6
{(-1 + t) t (1 - 5 t + 13 t - 17 t + 13 t - 5 t + t ),
2 3 4 5 6
1 - 5 t + 13 t - 17 t + 13 t - 5 t + t
-------------------------------------------}
3
t
|