In 2007, Jean-Marie Droz of the University of Zurich (working along with Anna Beliakova) wrote a Python program to compute the (hat-version) Heegaard-Floer Knot Homology Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}(K)}
of a knot 
(see arXiv:0803.2379). His program is integrated into KnotTheory`, though to run it, you must have Python as well as the Python library Psyco installed on your system.
(For In[1] see Setup)
| In[1]:=
|
?HFKHat
|
| HFKHat[K][t,m] returns the Poincare polynomial of the Heegaard-Floer Knot Homology (hat version) of the knot K, in the Alexander variable t and the Maslov variable m.
|
|
| In[2]:=
|
HFKHat::about
|
| The Heegaard-Floer Knot Homology program was written by Jean-Marie Droz in 2007 at the University of Zurich, based on methods of Anna Beliakova's arXiv:07050669.
|
|
The Heegaard-Floer Knot Homology is a categorification of the Alexander polynomial. Let us test that for the knot 8_19:
In[3]:=
|
hfk = HFKHat[K = Knot[8, 19]][t, m]
|
Out[3]=
|
2 -3 m 5 2 6 3
m + t + -- + m t + m t
2
t
|
In[4]:=
|
{hfk /. m -> -1, Alexander[K][t]}
|
Out[4]=
|
-3 -2 2 3 -3 -2 2 3
{1 + t - t - t + t , 1 + t - t - t + t }
|
The knot 8_19 is the first knot in the Rolfsen Knot Table whose Heegaard-Floer Knot Homology is not "diagonal". Let us test that. The homology Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}(K)}
is "on diagonal", iff its Poincare polynomial, evaluated at Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=1/t}
, is a monomial:
In[5]:=
|
Select[AllKnots[{3, 8}], (Head[HFKHat[#][t, 1/t]] == Plus) &]
|
Out[5]=
|
{Knot[8, 19]}
|
In[6]:=
|
hfk /. m -> 1/t
|
Out[6]=
|
4 -2
-- + t
3
t
|
The (mirrored) Conway knot K11n34 and the (mirrored) Kinoshita-Terasaka knot K11n42 are a mutant pair, and are notoriously difficult to tell apart. Let us check that an array of standard knot polynomials fails to separate them, yet Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}}
succeeds:
In[7]:=
|
K1 = Knot["K11n34"]; K2 = Knot["K11n42"];
test[invt_] := (invt[K1] =!= invt[K2]);
test /@ {
Alexander, MultivariableAlexander, Jones, HOMFLYPT, Kauffman, Kh, HFKHat
}
|
Out[7]=
|
{False, False, False, False, False, False, True}
|
Indeed,
In[8]:=
|
{HFKHat[K1][t, m], HFKHat[K2][t, m]}
|
Out[8]=
|
2 1 1 3 3 3 3
{3 + - + ----- + ----- + ----- + ----- + ---- + --- + 3 t + 3 m t +
m 4 3 3 3 3 2 2 2 2 m t
m t m t m t m t m t
2 2 2 2 3 3 3
3 m t + 3 m t + m t + m t ,
6 1 1 4 4 2 2 2
7 + - + ----- + ----- + ---- + --- + 4 t + 4 m t + m t + m t }
m 3 2 2 2 2 m t
m t m t m t
|
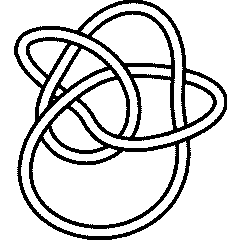
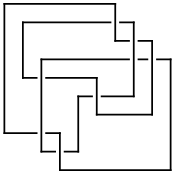
On July 6, 2006, User:AnonMoos asked User:Drorbn if he could identify the knot in the left hand side picture below. At the time it was impossible using the tools available with KnotTheory` - using any of many invariants, the answer can be found to be either the mirror of K11n34 or the mirror of K11n42, but KnotTheory` couldn't tell which one it is (though of course, it is possible to do it "by hand"). The 2007 addition Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}}
does the job, though. Indeed, we first extract the mystery knot's DT (Dowker-Thistlethwaite) Code using the picture on the right hand side below, then compute Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}}
, and then search for it within the Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{\operatorname{HFK}}}
's of all knots with up to 11 crossings:
|
|
In[9]:=
|
K3 = DTCode[6, 8, 14, 12, 4, -18, 2, -20, -22, -10, -16];
|
In[10]:=
|
H = HFKHat[Mirror[K3]][t, m]
|
Out[10]=
|
2 1 1 3 3 3 3
3 + - + ----- + ----- + ----- + ----- + ---- + --- + 3 t + 3 m t +
m 4 3 3 3 3 2 2 2 2 m t
m t m t m t m t m t
2 2 2 2 3 3 3
3 m t + 3 m t + m t + m t
|
In[11]:=
|
Select[AllKnots[], HFKHat[#][t, m] == H &]
|
Out[11]=
|
{Knot[11, NonAlternating, 34]}
|
And so the mystery knot is the Conway knot, the mirror of K11n34.
