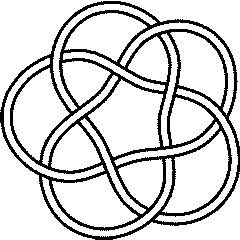10 124

10_123

10_125

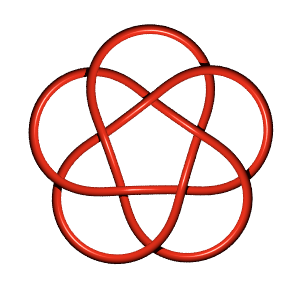
Visit 10 124's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit 10 124's page at Knotilus! Visit 10 124's page at the original Knot Atlas! 10_124 is also known as the torus knot T(5,3) or the pretzel knot P(5,3,-2). It is one of two knots which are both torus knots and pretzel knots, the other being 8_19 = T(4,3) = P(3,3,-2). It seems like the prior statement is incorrect. I suspect what this should say is 10_124 and 8_19 are the only torus knots which are also almost alternating. See page 108 in the Encyclopedia of Knot Theory. Confirmation of this is that 3_1 is the pretzel knot P(1,1,1), i.e., the right-handed trefoil. It looks like 5_1 is a pretzel knot also, and so on, i.e. 7_1, 9_1, and should include the Hopf link and the Solomon link etc. These are torus knots/links also.

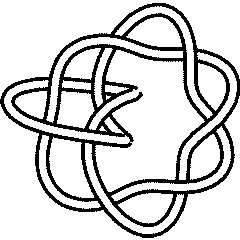
If one takes the symmetric diagram for 10_123 and makes it doubly alternating one gets a diagram for 10_124. That's the torus knot view. There is then a nice representation of the quandle of 10_124 into the dodecahedral quandle $Q_{30}$. See [1].

10_124 is not $k$-colourable for any $k$. See The Determinant and the Signature.

Torus knot T(5,3) form

Knot presentations

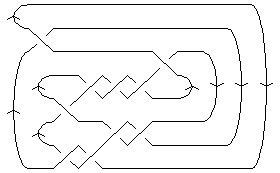
Planar diagram presentation	X4251 X8493 X9,17,10,16 X5,15,6,14 X15,7,16,6 X11,19,12,18 X13,1,14,20 X17,11,18,10 X19,13,20,12 X2837
Gauss code	1, -10, 2, -1, -4, 5, 10, -2, -3, 8, -6, 9, -7, 4, -5, 3, -8, 6, -9, 7
Dowker-Thistlethwaite code	4 8 -14 2 -16 -18 -20 -6 -10 -12
Conway Notation	[5,3,2-]

Minimum Braid Representative: Length is 10, width is 3. Braid index is 3.

A Morse Link Presentation:

Three dimensional invariants

Symmetry type Reversible Unknotting number 4 3-genus 4 Bridge index 3 Super bridge index Missing Nakanishi index 1 Maximal Thurston-Bennequin number [7][-15] Hyperbolic Volume Not hyperbolic A-Polynomial See Data:10 124/A-polynomial

[edit Notes for 10 124's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus $4$ Topological 4 genus $4$ Concordance genus $4$ Rasmussen s-Invariant -8

[edit Notes for 10 124's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$t^{4}-t^{3}+t-1+t^{-1}-t^{-3}+t^{-4}$
Conway polynomial	$z^{8}+7z^{6}+14z^{4}+8z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 1, 8 }
Jones polynomial	$-q^{10}+q^{6}+q^{4}$
HOMFLY-PT polynomial (db, data sources)	$z^{8}a^{-8}+8z^{6}a^{-8}-z^{6}a^{-10}+21z^{4}a^{-8}-7z^{4}a^{-10}+21z^{2}a^{-8}-14z^{2}a^{-10}+z^{2}a^{-12}+7a^{-8}-8a^{-10}+2a^{-12}$
Kauffman polynomial (db, data sources)	$z^{8}a^{-8}+z^{8}a^{-10}+z^{7}a^{-9}+z^{7}a^{-11}-8z^{6}a^{-8}-8z^{6}a^{-10}-7z^{5}a^{-9}-7z^{5}a^{-11}+21z^{4}a^{-8}+21z^{4}a^{-10}+14z^{3}a^{-9}+14z^{3}a^{-11}-21z^{2}a^{-8}-22z^{2}a^{-10}-z^{2}a^{-12}-8za^{-9}-8za^{-11}+7a^{-8}+8a^{-10}+2a^{-12}$
The A2 invariant	$q^{-14}+q^{-16}+2q^{-18}+2q^{-20}+2q^{-22}+q^{-24}-2q^{-28}-2q^{-30}-2q^{-32}-q^{-34}+q^{-40}$
The G2 invariant	$q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}+2q^{-80}+2q^{-82}+q^{-84}+2q^{-86}+2q^{-88}+2q^{-90}+2q^{-92}+2q^{-94}+q^{-96}+2q^{-98}+q^{-100}+q^{-104}+q^{-106}-q^{-112}-q^{-114}-q^{-118}-2q^{-120}-2q^{-122}-q^{-124}-q^{-126}-2q^{-128}-2q^{-130}-2q^{-132}-q^{-134}-q^{-136}-2q^{-138}-2q^{-140}-q^{-142}-q^{-146}-q^{-148}+q^{-160}+q^{-162}+q^{-168}+q^{-170}+q^{-180}$

Further Quantum Invariants[show]

Further quantum knot invariants for 10_124.

A1 Invariants.

Weight	Invariant
1	$q^{-7}+q^{-9}+q^{-11}+q^{-13}-q^{-19}-q^{-21}$
2	$q^{-14}+q^{-16}+q^{-18}+q^{-20}+q^{-22}+q^{-24}+q^{-26}-q^{-36}-q^{-38}-q^{-40}-q^{-42}-q^{-44}+q^{-60}$
3	$q^{-21}+q^{-23}+q^{-25}+q^{-27}+q^{-29}+q^{-31}+q^{-33}+q^{-35}+q^{-37}+q^{-39}-q^{-53}-q^{-55}-q^{-57}-q^{-59}-q^{-61}-q^{-63}-q^{-65}-q^{-67}+q^{-97}+q^{-99}+q^{-101}+q^{-103}-q^{-109}-q^{-111}$
5	$q^{-35}+q^{-37}+q^{-39}+q^{-41}+q^{-43}+q^{-45}+q^{-47}+q^{-49}+q^{-51}+q^{-53}+q^{-55}+q^{-57}+q^{-59}+q^{-61}+q^{-63}+q^{-65}-q^{-87}-q^{-89}-q^{-91}-q^{-93}-q^{-95}-q^{-97}-q^{-99}-q^{-101}-q^{-103}-q^{-105}-q^{-107}-q^{-109}-q^{-111}-q^{-113}+q^{-171}+q^{-173}+q^{-175}+q^{-177}+q^{-179}+q^{-181}+q^{-183}+q^{-185}+q^{-187}+q^{-189}-q^{-203}-q^{-205}-q^{-207}-q^{-209}-q^{-211}-q^{-213}-q^{-215}-q^{-217}+q^{-247}+q^{-249}+q^{-251}+q^{-253}-q^{-259}-q^{-261}$
6	$q^{-42}+q^{-44}+q^{-46}+q^{-48}+q^{-50}+q^{-52}+q^{-54}+q^{-56}+q^{-58}+q^{-60}+q^{-62}+q^{-64}+q^{-66}+q^{-68}+q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}-q^{-104}-q^{-106}-q^{-108}-q^{-110}-q^{-112}-q^{-114}-q^{-116}-q^{-118}-q^{-120}-q^{-122}-q^{-124}-q^{-126}-q^{-128}-q^{-130}-q^{-132}-q^{-134}-q^{-136}+q^{-208}+q^{-210}+q^{-212}+q^{-214}+q^{-216}+q^{-218}+q^{-220}+q^{-222}+q^{-224}+q^{-226}+q^{-228}+q^{-230}+q^{-232}-q^{-250}-q^{-252}-q^{-254}-q^{-256}-q^{-258}-q^{-260}-q^{-262}-q^{-264}-q^{-266}-q^{-268}-q^{-270}+q^{-314}+q^{-316}+q^{-318}+q^{-320}+q^{-322}+q^{-324}+q^{-326}-q^{-336}-q^{-338}-q^{-340}-q^{-342}-q^{-344}+q^{-360}$

A2 Invariants.

Weight	Invariant
1,0	$q^{-14}+q^{-16}+2q^{-18}+2q^{-20}+2q^{-22}+q^{-24}-2q^{-28}-2q^{-30}-2q^{-32}-q^{-34}+q^{-40}$
1,1	$q^{-28}+2q^{-30}+4q^{-32}+6q^{-34}+7q^{-36}+8q^{-38}+6q^{-40}+4q^{-42}+q^{-44}-2q^{-46}-6q^{-48}-8q^{-50}-9q^{-52}-8q^{-54}-6q^{-56}-4q^{-58}-2q^{-60}+2q^{-64}+2q^{-66}+4q^{-68}+4q^{-70}+4q^{-72}+2q^{-74}+q^{-76}-2q^{-78}-2q^{-80}-2q^{-82}-q^{-84}+2q^{-90}$
2,0	$q^{-28}+q^{-30}+2q^{-32}+2q^{-34}+3q^{-36}+3q^{-38}+4q^{-40}+3q^{-42}+3q^{-44}+2q^{-46}+2q^{-48}-q^{-52}-3q^{-54}-4q^{-56}-5q^{-58}-5q^{-60}-5q^{-62}-4q^{-64}-3q^{-66}-2q^{-68}-q^{-70}+2q^{-74}+2q^{-76}+4q^{-78}+4q^{-80}+4q^{-82}+2q^{-84}+q^{-86}-2q^{-88}-2q^{-90}-2q^{-92}-q^{-94}+q^{-100}$

A3 Invariants.

Weight	Invariant
0,1,0	$q^{-28}+q^{-30}+3q^{-32}+4q^{-34}+6q^{-36}+6q^{-38}+7q^{-40}+3q^{-42}+q^{-44}-4q^{-46}-7q^{-48}-9q^{-50}-9q^{-52}-6q^{-54}-3q^{-56}+q^{-58}+3q^{-60}+4q^{-62}+2q^{-64}+2q^{-66}$
1,0,0	$q^{-21}+q^{-23}+2q^{-25}+3q^{-27}+3q^{-29}+3q^{-31}+2q^{-33}-2q^{-37}-3q^{-39}-4q^{-41}-3q^{-43}-2q^{-45}+q^{-49}+q^{-51}+q^{-53}$
1,0,1	$q^{-42}+2q^{-44}+5q^{-46}+9q^{-48}+14q^{-50}+19q^{-52}+23q^{-54}+22q^{-56}+19q^{-58}+10q^{-60}-q^{-62}-14q^{-64}-26q^{-66}-34q^{-68}-38q^{-70}-35q^{-72}-26q^{-74}-13q^{-76}-q^{-78}+11q^{-80}+18q^{-82}+21q^{-84}+19q^{-86}+14q^{-88}+8q^{-90}+4q^{-92}-3q^{-96}-3q^{-98}-4q^{-100}-3q^{-102}-3q^{-104}-q^{-106}-q^{-108}+2q^{-120}$

A4 Invariants.

Weight	Invariant
0,1,0,0	$q^{-42}+q^{-44}+3q^{-46}+5q^{-48}+8q^{-50}+10q^{-52}+14q^{-54}+13q^{-56}+13q^{-58}+8q^{-60}+2q^{-62}-7q^{-64}-14q^{-66}-21q^{-68}-23q^{-70}-21q^{-72}-16q^{-74}-8q^{-76}-q^{-78}+7q^{-80}+9q^{-82}+11q^{-84}+9q^{-86}+7q^{-88}+3q^{-90}+2q^{-92}-q^{-96}-q^{-98}-q^{-100}-q^{-102}-q^{-104}$
1,0,0,0	$q^{-28}+q^{-30}+2q^{-32}+3q^{-34}+4q^{-36}+4q^{-38}+4q^{-40}+2q^{-42}+q^{-44}-2q^{-46}-4q^{-48}-5q^{-50}-5q^{-52}-4q^{-54}-2q^{-56}+q^{-60}+2q^{-62}+q^{-64}+q^{-66}$

B2 Invariants.

Weight	Invariant
0,1	$q^{-28}+q^{-30}+q^{-32}+2q^{-34}+2q^{-36}+2q^{-38}+q^{-40}+q^{-42}+q^{-44}-q^{-48}-q^{-50}-q^{-52}-2q^{-54}-q^{-56}-q^{-58}-q^{-60}$
1,0	$q^{-42}+q^{-46}+q^{-48}+2q^{-50}+q^{-52}+3q^{-54}+2q^{-56}+3q^{-58}+2q^{-60}+3q^{-62}+2q^{-64}+2q^{-66}-q^{-72}-2q^{-74}-3q^{-76}-3q^{-78}-3q^{-80}-4q^{-82}-3q^{-84}-3q^{-86}-2q^{-88}-2q^{-90}+q^{-96}+q^{-98}+2q^{-100}+q^{-102}+q^{-104}+q^{-106}+q^{-108}$

D4 Invariants.

Weight	Invariant
1,0,0,0	$q^{-42}+q^{-44}+2q^{-46}+4q^{-48}+5q^{-50}+7q^{-52}+8q^{-54}+8q^{-56}+7q^{-58}+5q^{-60}+q^{-62}-3q^{-64}-7q^{-66}-10q^{-68}-11q^{-70}-11q^{-72}-9q^{-74}-6q^{-76}-2q^{-78}+q^{-80}+3q^{-82}+4q^{-84}+4q^{-86}+3q^{-88}+2q^{-90}+q^{-92}$

G2 Invariants.

Weight	Invariant
1,0	$q^{-70}+q^{-72}+q^{-74}+q^{-76}+q^{-78}+2q^{-80}+2q^{-82}+q^{-84}+2q^{-86}+2q^{-88}+2q^{-90}+2q^{-92}+2q^{-94}+q^{-96}+2q^{-98}+q^{-100}+q^{-104}+q^{-106}-q^{-112}-q^{-114}-q^{-118}-2q^{-120}-2q^{-122}-q^{-124}-q^{-126}-2q^{-128}-2q^{-130}-2q^{-132}-q^{-134}-q^{-136}-2q^{-138}-2q^{-140}-q^{-142}-q^{-146}-q^{-148}+q^{-160}+q^{-162}+q^{-168}+q^{-170}+q^{-180}$

.

Computer Talk[show]

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["10 124"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$t^{4}-t^{3}+t-1+t^{-1}-t^{-3}+t^{-4}$

In[5]:=

Conway[K][z]

Out[5]=

$z^{8}+7z^{6}+14z^{4}+8z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 1, 8 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$-q^{10}+q^{6}+q^{4}$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$z^{8}a^{-8}+8z^{6}a^{-8}-z^{6}a^{-10}+21z^{4}a^{-8}-7z^{4}a^{-10}+21z^{2}a^{-8}-14z^{2}a^{-10}+z^{2}a^{-12}+7a^{-8}-8a^{-10}+2a^{-12}$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$z^{8}a^{-8}+z^{8}a^{-10}+z^{7}a^{-9}+z^{7}a^{-11}-8z^{6}a^{-8}-8z^{6}a^{-10}-7z^{5}a^{-9}-7z^{5}a^{-11}+21z^{4}a^{-8}+21z^{4}a^{-10}+14z^{3}a^{-9}+14z^{3}a^{-11}-21z^{2}a^{-8}-22z^{2}a^{-10}-z^{2}a^{-12}-8za^{-9}-8za^{-11}+7a^{-8}+8a^{-10}+2a^{-12}$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {...}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {...}

Vassiliev invariants

V2 and V3:

(8, 20)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $32$ $160$ $512$ ${\frac {3184}{3}}$ ${\frac {416}{3}}$ $5120$ ${\frac {23680}{3}}$ ${\frac {4000}{3}}$ $832$ ${\frac {16384}{3}}$ $12800$ ${\frac {101888}{3}}$ ${\frac {13312}{3}}$ ${\frac {910684}{15}}$ ${\frac {59264}{15}}$ ${\frac {869536}{45}}$ ${\frac {2756}{9}}$ ${\frac {34684}{15}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$8 is the signature of 10 124. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ 0 1 2 3 4 5 6 7 χ 21               1 -1 19           1     -1 17           1 1   0 15       1 1       0 13         1       1 11     1           1 9 1               1 7 1               1

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=5$ $i=7$ $i=9$ $r=0$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=1$ $r=2$ ${\mathbb {Z} }$ $r=3$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=4$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=5$ ${\mathbb {Z} }$ ${\mathbb {Z} }$ $r=6$ ${\mathbb {Z} }$ $r=7$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the $n+1$-dimensional representation of $sl(2)$)[show]

$n$	$J_{n}$
2	$q^{29}-q^{28}+q^{26}-q^{25}+q^{23}-q^{22}-q^{21}+q^{20}-q^{19}-q^{18}+q^{17}-q^{15}+q^{14}+q^{11}+q^{8}$
3	$-q^{54}+q^{52}+q^{48}-q^{46}+q^{44}-q^{42}+q^{40}-q^{38}+q^{36}-q^{34}-q^{30}-q^{26}+q^{24}-q^{22}+q^{20}+q^{16}+q^{12}$
4	$q^{88}-q^{87}+q^{83}-q^{82}-q^{80}+q^{78}-q^{77}+q^{73}-q^{72}+q^{71}+q^{68}-q^{67}+q^{66}-q^{64}+q^{63}-q^{62}+q^{61}-q^{59}+q^{58}-q^{57}+q^{56}-q^{54}+q^{53}-q^{52}+q^{51}-q^{49}+q^{48}-q^{47}+q^{46}-q^{44}-q^{42}+q^{41}-q^{39}-q^{37}+q^{36}-q^{34}+q^{31}-q^{29}+q^{26}+q^{21}+q^{16}$
5	$-q^{128}+q^{126}+q^{124}-q^{122}+q^{118}-q^{116}+q^{112}-q^{110}-q^{104}+q^{92}+q^{86}-q^{82}+q^{80}-q^{76}+q^{74}-q^{70}+q^{68}-q^{64}+q^{62}-q^{58}+q^{56}-q^{54}-q^{52}+q^{50}-q^{48}-q^{46}+q^{44}-q^{42}+q^{38}-q^{36}+q^{32}+q^{26}+q^{20}$
6	$q^{177}-q^{176}+q^{170}-2q^{169}+q^{164}+q^{163}-2q^{162}+q^{160}+q^{157}+q^{156}-2q^{155}+q^{150}+q^{149}-2q^{148}+q^{143}+q^{142}-2q^{141}+q^{136}+q^{135}-2q^{134}-q^{132}+q^{129}+q^{128}-2q^{127}-q^{125}+q^{122}+2q^{121}-2q^{120}-q^{118}+q^{115}+2q^{114}-q^{113}-q^{111}+q^{108}+2q^{107}-q^{106}-q^{104}+q^{101}+q^{100}-q^{99}-q^{97}+q^{94}+q^{93}-q^{92}-q^{90}+q^{87}+q^{86}-q^{85}-q^{83}+q^{80}+q^{79}-q^{78}-q^{76}+q^{73}+q^{72}-q^{71}-q^{69}+q^{66}-q^{64}-q^{62}+q^{59}-q^{57}-q^{55}+q^{52}-q^{50}+q^{45}-q^{43}+q^{38}+q^{31}+q^{24}$
7	$-q^{232}+q^{230}+q^{228}-2q^{224}+q^{222}+q^{220}-2q^{216}+q^{214}+q^{212}-q^{210}-2q^{208}+q^{206}+q^{204}-2q^{200}+q^{198}+2q^{196}-2q^{192}+q^{190}+2q^{188}-q^{186}-2q^{184}+q^{182}+2q^{180}-q^{178}-2q^{176}+q^{174}+2q^{172}-q^{170}-2q^{168}+q^{166}+2q^{164}-q^{162}-2q^{160}+2q^{156}-q^{154}-2q^{152}+2q^{148}-q^{146}-q^{144}+2q^{140}-q^{138}-q^{136}+q^{134}+2q^{132}-q^{130}-q^{128}+q^{126}+2q^{124}-q^{122}-q^{120}+2q^{116}-q^{114}-q^{112}+2q^{108}-q^{106}-q^{104}+2q^{100}-q^{98}-q^{96}+2q^{92}-q^{90}-q^{88}+2q^{84}-q^{82}-q^{80}+q^{76}-q^{74}-q^{72}+q^{68}-q^{66}-q^{64}+q^{60}-q^{58}+q^{52}-q^{50}+q^{44}+q^{36}+q^{28}$

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 29, 2005, 15:27:48)...
In[2]:=	PD[Knot[10, 124]]
Out[2]=	PD[X[4, 2, 5, 1], X[8, 4, 9, 3], X[9, 17, 10, 16], X[5, 15, 6, 14], X[15, 7, 16, 6], X[11, 19, 12, 18], X[13, 1, 14, 20], X[17, 11, 18, 10], X[19, 13, 20, 12], X[2, 8, 3, 7]]
In[3]:=	GaussCode[Knot[10, 124]]
Out[3]=	GaussCode[1, -10, 2, -1, -4, 5, 10, -2, -3, 8, -6, 9, -7, 4, -5, 3, -8, 6, -9, 7]
In[4]:=	DTCode[Knot[10, 124]]
Out[4]=	DTCode[4, 8, -14, 2, -16, -18, -20, -6, -10, -12]
In[5]:=	br = BR[Knot[10, 124]]
Out[5]=	BR[3, {1, 1, 1, 1, 1, 2, 1, 1, 1, 2}]
In[6]:=	{First[br], Crossings[br]}
Out[6]=	{3, 10}
In[7]:=	BraidIndex[Knot[10, 124]]
Out[7]=	3
In[8]:=	Show[DrawMorseLink[Knot[10, 124]]]
Out[8]=	-Graphics-
In[9]:=	(#[Knot[10, 124]]&) /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}
Out[9]=	{Reversible, 4, 4, 3, NotAvailable, 1}
In[10]:=	alex = Alexander[Knot[10, 124]][t]
Out[10]=	-4 -3 1 3 4 -1 + t - t + - + t - t + t t
In[11]:=	Conway[Knot[10, 124]][z]
Out[11]=	2 4 6 8 1 + 8 z + 14 z + 7 z + z
In[12]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[12]=	{Knot[10, 124]}
In[13]:=	{KnotDet[Knot[10, 124]], KnotSignature[Knot[10, 124]]}
Out[13]=	{1, 8}
In[14]:=	Jones[Knot[10, 124]][q]
Out[14]=	4 6 10 q + q - q
In[15]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[15]=	{Knot[10, 124]}
In[16]:=	A2Invariant[Knot[10, 124]][q]
Out[16]=	14 16 18 20 22 24 28 30 32 34 q + q + 2 q + 2 q + 2 q + q - 2 q - 2 q - 2 q - q + 40 q
In[17]:=	HOMFLYPT[Knot[10, 124]][a, z]
Out[17]=	2 2 2 4 4 6 6 8 2 8 7 z 14 z 21 z 7 z 21 z z 8 z z --- - --- + -- + --- - ----- + ----- - ---- + ----- - --- + ---- + -- 12 10 8 12 10 8 10 8 10 8 8 a a a a a a a a a a a
In[18]:=	Kauffman[Knot[10, 124]][a, z]
Out[18]=	2 2 2 3 3 2 8 7 8 z 8 z z 22 z 21 z 14 z 14 z --- + --- + -- - --- - --- - --- - ----- - ----- + ----- + ----- + 12 10 8 11 9 12 10 8 11 9 a a a a a a a a a a 4 4 5 5 6 6 7 7 8 8 21 z 21 z 7 z 7 z 8 z 8 z z z z z ----- + ----- - ---- - ---- - ---- - ---- + --- + -- + --- + -- 10 8 11 9 10 8 11 9 10 8 a a a a a a a a a a
In[19]:=	{Vassiliev[2][Knot[10, 124]], Vassiliev[3][Knot[10, 124]]}
Out[19]=	{8, 20}
In[20]:=	Kh[Knot[10, 124]][q, t]
Out[20]=	7 9 11 2 15 3 13 4 15 4 17 5 19 5 q + q + q t + q t + q t + q t + q t + q t + 17 6 21 7 q t + q t
In[21]:=	ColouredJones[Knot[10, 124], 2][q]
Out[21]=	8 11 14 15 17 18 19 20 21 22 23 25 q + q + q - q + q - q - q + q - q - q + q - q + 26 28 29 q - q + q

See/edit the Rolfsen_Splice_Template. Back to the top.

10_123 10_125