Braid Representatives: Difference between revisions
No edit summary |
DrorsRobot (talk | contribs) No edit summary |
||
| Line 7: | Line 7: | ||
<!--$$?BR$$--> |
<!--$$?BR$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpAndAbout| |
|||
{{HelpAndAbout1|n=1|s=BR}} |
|||
n = 1 | |
|||
| ⚫ | BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |
||
n1 = 2 | |
|||
{{HelpAndAbout2|n=2|s=BR}} |
|||
in = <nowiki>BR</nowiki> | |
|||
| ⚫ | |||
| ⚫ | out= <nowiki>BR stands for Braid Representative. BR[k,l] represents a braid on k strands with crossings l={i1,i2,...}, where a positive index i within the list l indicates a right-handed crossing between strand number i and strand number i+1 and a negative i indicates a left handed crossing between strands numbers |i| and |i|+1. Each ij can also be a list of non-adjacent (i.e., commuting) indices. BR also acts as a "type caster": BR[K] will return a braid whose closure is K if K is given in any format that KnotTheory` understands. BR[K] where K is is a named knot with up to 10 crossings returns a minimum braid representative for that knot.</nowiki> | |
||
{{HelpAndAbout3}} |
|||
| ⚫ | |||
<!--END--> |
<!--END--> |
||
<!--$$?Mirror$$--> |
<!--$$?Mirror$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
|||
{{Help1|n=3|s=Mirror}} |
|||
n = 3 | |
|||
| ⚫ | |||
in = <nowiki>Mirror</nowiki> | |
|||
{{Help2}} |
|||
| ⚫ | |||
<!--END--> |
<!--END--> |
||
| Line 25: | Line 27: | ||
<!--$$br1 = BR[2, {-1, -1, -1}];$$--> |
<!--$$br1 = BR[2, {-1, -1, -1}];$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{In| |
||
n = 4 | |
|||
in = <nowiki>br1 = BR[2, {-1, -1, -1}];</nowiki>}} |
|||
{{In2}} |
|||
<!--END--> |
<!--END--> |
||
| Line 33: | Line 35: | ||
<!--$$PD[br1]$$--> |
<!--$$PD[br1]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{InOut| |
||
n = 5 | |
|||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>PD[br1]</nowiki></pre> |
|||
in = <nowiki>PD[br1]</nowiki> | |
|||
out= <nowiki>PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]</nowiki>}} |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$Jones[br1][q]$$--> |
<!--$$Jones[br1][q]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{InOut| |
||
n = 6 | |
|||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>Jones[br1][q]</nowiki></pre> |
|||
in = <nowiki>Jones[br1][q]</nowiki> | |
|||
{{InOut2|n=6}}<pre style="border: 0px; padding: 0em"><nowiki> -4 -3 1 |
|||
out= <nowiki> -4 -3 1 |
|||
-q + q + - |
-q + q + - |
||
q</nowiki> |
q</nowiki>}} |
||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$Mirror[br1]$$--> |
<!--$$Mirror[br1]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{InOut| |
||
n = 7 | |
|||
<pre style="color: red; border: 0px; padding: 0em"><nowiki>Mirror[br1]</nowiki></pre> |
|||
in = <nowiki>Mirror[br1]</nowiki> | |
|||
out= <nowiki>BR[2, {1, 1, 1}]</nowiki>}} |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
| Line 61: | Line 63: | ||
<!--$$BR[TorusKnot[5, 4]]$$--> |
<!--$$BR[TorusKnot[5, 4]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{InOut| |
||
n = 8 | |
|||
in = <nowiki>BR[TorusKnot[5, 4]]</nowiki> | |
|||
out= <nowiki>BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]</nowiki>}} |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
| Line 71: | Line 73: | ||
<!--$$br2 = BR[Knot[10, 1]]$$--> |
<!--$$br2 = BR[Knot[10, 1]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{ |
{{InOut| |
||
n = 9 | |
|||
in = <nowiki>br2 = BR[Knot[10, 1]]</nowiki> | |
|||
out= <nowiki>BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]</nowiki>}} |
|||
{{InOut3}} |
|||
<!--END--> |
<!--END--> |
||
<!--$$Show[BraidPlot[CollapseBraid[br2]]]$$--> |
<!--$$Show[BraidPlot[CollapseBraid[br2]]]$$--> |
||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{Graphics| |
|||
{{Graphics1|n=10}} |
|||
n = 11 | |
|||
Show[BraidPlot[CollapseBraid[br2]]] |
in = <nowiki>Show[BraidPlot[CollapseBraid[br2]]]</nowiki> | |
||
img= Braid_Representatives_Out_10.gif | |
|||
out= <nowiki>-Graphics-</nowiki>}} |
|||
<!--END--> |
<!--END--> |
||
Revision as of 11:52, 30 August 2005
Every knot and every link is the closure of a braid. KnotTheory` can also represent knots and links as braid closures:
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus for example,
In[4]:=
|
br1 = BR[2, {-1, -1, -1}];
|
In[5]:=
|
PD[br1]
|
Out[5]=
|
PD[X[6, 3, 1, 4], X[4, 1, 5, 2], X[2, 5, 3, 6]]
|
In[6]:=
|
Jones[br1][q]
|
Out[6]=
|
-4 -3 1
-q + q + -
q
|
In[7]:=
|
Mirror[br1]
|
Out[7]=
|
BR[2, {1, 1, 1}]
|
KnotTheory` has the braid representatives of some knots and links pre-loaded. Thus for example,
In[8]:=
|
BR[TorusKnot[5, 4]]
|
Out[8]=
|
BR[4, {1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3}]
|
The minimum braid representative of a given knot is a braid representative for that knot which has a minimal number of braid crossings and within those braid representatives with a minimal number of braid crossings, it has a minimal number of strands (full details are in [Gittings]). Thomas Gittings kindly provided us the minimum braid representatives for all knots with up to 10 crossings. Thus for example, the minimum braid representative for the knot Template:10 1 has length (number of crossings) 13 and width 6 (number of strands, also see Invariants from Braid Theory):
In[9]:=
|
br2 = BR[Knot[10, 1]]
|
Out[9]=
|
BR[6, {-1, -1, -2, 1, -2, -3, 2, -3, -4, 3, 5, -4, 5}]
|
In[11]:=
|
Show[BraidPlot[CollapseBraid[br2]]]
|
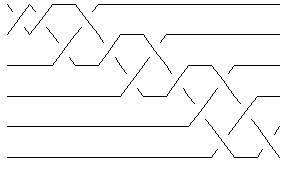
| |
Out[11]=
|
-Graphics-
|
(Check Drawing Braids for information about the command BraidPlot and the related command CollapseBraid.)
[Gittings] ^ T. A. Gittings, Minimum braids: a complete invariant of knots and links, arXiv:math.GT/0401051.