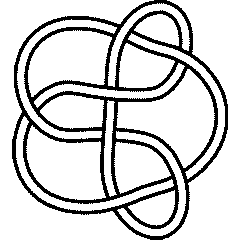|
|
| Line 1: |
Line 1: |
|
|
<!-- WARNING! WARNING! WARNING! |
|
<!-- This page was generated from the splice template "Rolfsen_Splice_Template". Please do not edit! --> |
|
<!-- This page was generated from the splice template [[Rolfsen_Splice_Base]]. Please do not edit! |
|
<!-- --> <!-- |
|
|
|
<!-- You probably want to edit the template referred to immediately below. (See [[Category:Knot Page Template]].) |
|
--> |
|
|
|
<!-- This page itself was created by running [[Media:KnotPageSpliceRobot.nb]] on [[Rolfsen_Splice_Base]]. --> |
|
|
<!-- <math>\text{Null}</math> --> |
|
|
<!-- <math>\text{Null}</math> --> |
|
{{Rolfsen Knot Page| |
|
{{Rolfsen Knot Page| |
|
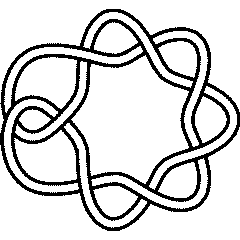
n = 8 | |
|
n = 8 | |
| Line 42: |
Line 45: |
|
coloured_jones_5 = <math>q^{30}-q^{29}+q^{24}-2 q^{23}+q^{21}+q^{19}+q^{18}-4 q^{17}-q^{16}+2 q^{15}+2 q^{14}+2 q^{13}+q^{12}-6 q^{11}-3 q^{10}+4 q^9+4 q^8+3 q^7-2 q^6-8 q^5-3 q^4+6 q^3+7 q^2+3 q-5-11 q^{-1} -3 q^{-2} +9 q^{-3} +9 q^{-4} +4 q^{-5} -7 q^{-6} -13 q^{-7} -5 q^{-8} +9 q^{-9} +12 q^{-10} +5 q^{-11} -7 q^{-12} -13 q^{-13} -5 q^{-14} +7 q^{-15} +13 q^{-16} +5 q^{-17} -7 q^{-18} -11 q^{-19} -4 q^{-20} +5 q^{-21} +12 q^{-22} +4 q^{-23} -6 q^{-24} -10 q^{-25} -5 q^{-26} +4 q^{-27} +11 q^{-28} +5 q^{-29} -4 q^{-30} -10 q^{-31} -6 q^{-32} +3 q^{-33} +10 q^{-34} +6 q^{-35} -2 q^{-36} -9 q^{-37} -7 q^{-38} +2 q^{-39} +8 q^{-40} +6 q^{-41} -7 q^{-43} -7 q^{-44} +6 q^{-46} +6 q^{-47} + q^{-48} -4 q^{-49} -5 q^{-50} -2 q^{-51} +3 q^{-52} +5 q^{-53} + q^{-54} -2 q^{-55} -3 q^{-56} -2 q^{-57} + q^{-58} +3 q^{-59} + q^{-60} - q^{-61} -2 q^{-62} - q^{-63} + q^{-64} +2 q^{-65} + q^{-66} - q^{-67} -2 q^{-68} - q^{-69} +3 q^{-71} +2 q^{-72} - q^{-73} -2 q^{-74} -2 q^{-75} - q^{-76} +2 q^{-77} +3 q^{-78} - q^{-80} - q^{-81} -2 q^{-82} +2 q^{-84} + q^{-85} - q^{-88} - q^{-89} + q^{-90} </math> | |
|
coloured_jones_5 = <math>q^{30}-q^{29}+q^{24}-2 q^{23}+q^{21}+q^{19}+q^{18}-4 q^{17}-q^{16}+2 q^{15}+2 q^{14}+2 q^{13}+q^{12}-6 q^{11}-3 q^{10}+4 q^9+4 q^8+3 q^7-2 q^6-8 q^5-3 q^4+6 q^3+7 q^2+3 q-5-11 q^{-1} -3 q^{-2} +9 q^{-3} +9 q^{-4} +4 q^{-5} -7 q^{-6} -13 q^{-7} -5 q^{-8} +9 q^{-9} +12 q^{-10} +5 q^{-11} -7 q^{-12} -13 q^{-13} -5 q^{-14} +7 q^{-15} +13 q^{-16} +5 q^{-17} -7 q^{-18} -11 q^{-19} -4 q^{-20} +5 q^{-21} +12 q^{-22} +4 q^{-23} -6 q^{-24} -10 q^{-25} -5 q^{-26} +4 q^{-27} +11 q^{-28} +5 q^{-29} -4 q^{-30} -10 q^{-31} -6 q^{-32} +3 q^{-33} +10 q^{-34} +6 q^{-35} -2 q^{-36} -9 q^{-37} -7 q^{-38} +2 q^{-39} +8 q^{-40} +6 q^{-41} -7 q^{-43} -7 q^{-44} +6 q^{-46} +6 q^{-47} + q^{-48} -4 q^{-49} -5 q^{-50} -2 q^{-51} +3 q^{-52} +5 q^{-53} + q^{-54} -2 q^{-55} -3 q^{-56} -2 q^{-57} + q^{-58} +3 q^{-59} + q^{-60} - q^{-61} -2 q^{-62} - q^{-63} + q^{-64} +2 q^{-65} + q^{-66} - q^{-67} -2 q^{-68} - q^{-69} +3 q^{-71} +2 q^{-72} - q^{-73} -2 q^{-74} -2 q^{-75} - q^{-76} +2 q^{-77} +3 q^{-78} - q^{-80} - q^{-81} -2 q^{-82} +2 q^{-84} + q^{-85} - q^{-88} - q^{-89} + q^{-90} </math> | |
|
coloured_jones_6 = <math>q^{42}-q^{41}-q^{36}+2 q^{35}-2 q^{34}+q^{33}+q^{30}-2 q^{29}+2 q^{28}-4 q^{27}+2 q^{26}+q^{25}+q^{24}+3 q^{23}-3 q^{22}+q^{21}-7 q^{20}+3 q^{19}+q^{18}+2 q^{17}+5 q^{16}-4 q^{15}+q^{14}-9 q^{13}+5 q^{12}+q^{10}+5 q^9-5 q^8+3 q^7-8 q^6+8 q^5-2 q^4-3 q^3+3 q^2-6 q+6-5 q^{-1} +13 q^{-2} -3 q^{-3} -6 q^{-4} -9 q^{-6} +6 q^{-7} -3 q^{-8} +18 q^{-9} -2 q^{-10} -6 q^{-11} - q^{-12} -12 q^{-13} +3 q^{-14} -3 q^{-15} +20 q^{-16} - q^{-17} -5 q^{-18} -11 q^{-20} +2 q^{-21} -4 q^{-22} +18 q^{-23} -2 q^{-24} -5 q^{-25} + q^{-26} -10 q^{-27} +3 q^{-28} -5 q^{-29} +16 q^{-30} -2 q^{-31} -4 q^{-32} +2 q^{-33} -9 q^{-34} +3 q^{-35} -7 q^{-36} +14 q^{-37} - q^{-39} +3 q^{-40} -9 q^{-41} +2 q^{-42} -10 q^{-43} +11 q^{-44} +3 q^{-45} +2 q^{-46} +4 q^{-47} -9 q^{-48} -13 q^{-50} +9 q^{-51} +5 q^{-52} +5 q^{-53} +5 q^{-54} -9 q^{-55} - q^{-56} -15 q^{-57} +6 q^{-58} +6 q^{-59} +7 q^{-60} +7 q^{-61} -7 q^{-62} - q^{-63} -15 q^{-64} +2 q^{-65} +4 q^{-66} +7 q^{-67} +8 q^{-68} -4 q^{-69} + q^{-70} -14 q^{-71} - q^{-72} + q^{-73} +5 q^{-74} +7 q^{-75} - q^{-76} +5 q^{-77} -11 q^{-78} -2 q^{-79} - q^{-80} +2 q^{-81} +4 q^{-82} +7 q^{-84} -8 q^{-85} - q^{-86} - q^{-87} + q^{-89} +7 q^{-91} -7 q^{-92} +7 q^{-98} -6 q^{-99} - q^{-100} - q^{-101} + q^{-104} +7 q^{-105} -4 q^{-106} - q^{-107} -2 q^{-108} - q^{-109} - q^{-110} +6 q^{-112} - q^{-113} - q^{-115} - q^{-116} -2 q^{-117} - q^{-118} +3 q^{-119} + q^{-121} - q^{-124} - q^{-125} + q^{-126} </math> | |
|
coloured_jones_6 = <math>q^{42}-q^{41}-q^{36}+2 q^{35}-2 q^{34}+q^{33}+q^{30}-2 q^{29}+2 q^{28}-4 q^{27}+2 q^{26}+q^{25}+q^{24}+3 q^{23}-3 q^{22}+q^{21}-7 q^{20}+3 q^{19}+q^{18}+2 q^{17}+5 q^{16}-4 q^{15}+q^{14}-9 q^{13}+5 q^{12}+q^{10}+5 q^9-5 q^8+3 q^7-8 q^6+8 q^5-2 q^4-3 q^3+3 q^2-6 q+6-5 q^{-1} +13 q^{-2} -3 q^{-3} -6 q^{-4} -9 q^{-6} +6 q^{-7} -3 q^{-8} +18 q^{-9} -2 q^{-10} -6 q^{-11} - q^{-12} -12 q^{-13} +3 q^{-14} -3 q^{-15} +20 q^{-16} - q^{-17} -5 q^{-18} -11 q^{-20} +2 q^{-21} -4 q^{-22} +18 q^{-23} -2 q^{-24} -5 q^{-25} + q^{-26} -10 q^{-27} +3 q^{-28} -5 q^{-29} +16 q^{-30} -2 q^{-31} -4 q^{-32} +2 q^{-33} -9 q^{-34} +3 q^{-35} -7 q^{-36} +14 q^{-37} - q^{-39} +3 q^{-40} -9 q^{-41} +2 q^{-42} -10 q^{-43} +11 q^{-44} +3 q^{-45} +2 q^{-46} +4 q^{-47} -9 q^{-48} -13 q^{-50} +9 q^{-51} +5 q^{-52} +5 q^{-53} +5 q^{-54} -9 q^{-55} - q^{-56} -15 q^{-57} +6 q^{-58} +6 q^{-59} +7 q^{-60} +7 q^{-61} -7 q^{-62} - q^{-63} -15 q^{-64} +2 q^{-65} +4 q^{-66} +7 q^{-67} +8 q^{-68} -4 q^{-69} + q^{-70} -14 q^{-71} - q^{-72} + q^{-73} +5 q^{-74} +7 q^{-75} - q^{-76} +5 q^{-77} -11 q^{-78} -2 q^{-79} - q^{-80} +2 q^{-81} +4 q^{-82} +7 q^{-84} -8 q^{-85} - q^{-86} - q^{-87} + q^{-89} +7 q^{-91} -7 q^{-92} +7 q^{-98} -6 q^{-99} - q^{-100} - q^{-101} + q^{-104} +7 q^{-105} -4 q^{-106} - q^{-107} -2 q^{-108} - q^{-109} - q^{-110} +6 q^{-112} - q^{-113} - q^{-115} - q^{-116} -2 q^{-117} - q^{-118} +3 q^{-119} + q^{-121} - q^{-124} - q^{-125} + q^{-126} </math> | |
|
coloured_jones_7 = | |
|
coloured_jones_7 = <math>\textrm{NotAvailable}(q)</math> | |
|
computer_talk = |
|
computer_talk = |
|
<table> |
|
<table> |
| Line 49: |
Line 52: |
|
<td align=left><pre style="color: red; border: 0px; padding: 0em"><< KnotTheory`</pre></td> |
|
<td align=left><pre style="color: red; border: 0px; padding: 0em"><< KnotTheory`</pre></td> |
|
</tr> |
|
</tr> |
|
<tr valign=top><td colspan=2>Loading KnotTheory` (version of August 29, 2005, 15:33:11)...</td></tr> |
|
<tr valign=top><td colspan=2>Loading KnotTheory` (version of August 29, 2005, 15:27:48)...</td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[2]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>PD[Knot[8, 1]]</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[2]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>PD[Knot[8, 1]]</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[2]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>PD[X[1, 4, 2, 5], X[9, 12, 10, 13], X[3, 11, 4, 10], X[11, 3, 12, 2], |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[2]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>PD[X[1, 4, 2, 5], X[9, 12, 10, 13], X[3, 11, 4, 10], X[11, 3, 12, 2], |
| Line 65: |
Line 68: |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[7]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>5</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[7]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>5</nowiki></pre></td></tr> |
|
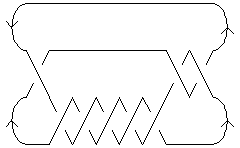
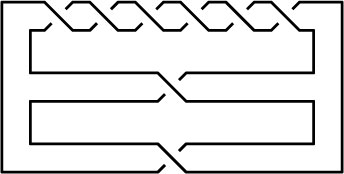
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[8]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>Show[DrawMorseLink[Knot[8, 1]]]</nowiki></pre></td></tr><tr><td></td><td align=left>[[Image:8_1_ML.gif]]</td></tr><tr valign=top><td><tt><font color=blue>Out[8]=</font></tt><td><tt><font color=black>-Graphics-</font></tt></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[8]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>Show[DrawMorseLink[Knot[8, 1]]]</nowiki></pre></td></tr><tr><td></td><td align=left>[[Image:8_1_ML.gif]]</td></tr><tr valign=top><td><tt><font color=blue>Out[8]=</font></tt><td><tt><font color=black>-Graphics-</font></tt></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[9]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>(#[Knot[8, 1]]&) /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[9]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki> (#[Knot[8, 1]]&) /@ { |
|
|
SymmetryType, UnknottingNumber, ThreeGenus, |
|
|
BridgeIndex, SuperBridgeIndex, NakanishiIndex |
|
|
}</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[9]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>{Reversible, 1, 1, 2, {4, 5}, 1}</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>Out[9]= </nowiki></pre></td><td><pre style="color: black; border: 0px; padding: 0em"><nowiki>{Reversible, 1, 1, 2, {4, 5}, 1}</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[10]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>alex = Alexander[Knot[8, 1]][t]</nowiki></pre></td></tr> |
|
<tr valign=top><td><pre style="color: blue; border: 0px; padding: 0em"><nowiki>In[10]:=</nowiki></pre></td><td><pre style="color: red; border: 0px; padding: 0em"><nowiki>alex = Alexander[Knot[8, 1]][t]</nowiki></pre></td></tr> |