R-Matrix Invariants: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
KnotTheory` can compute knot and link invariants associated with matrix solutions of the Yang-Baxter equation, using the program <code>REngine</code>: |
KnotTheory` can compute knot and link invariants associated with matrix solutions of the Yang-Baxter equation, using the program <code>REngine</code>: |
||
| Line 7: | Line 9: | ||
In more detail, let <math>V</math> be a free module of finite rank over a commutative ring, and let <math> R, \bar{R} \in End(V \otimes V) </math> be invertible. Further, let there be invertible endomorphisms <math>M_\leftarrow, M_\rightarrow, M^\leftarrow, M^\rightarrow \in End(V) </math>; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices. |
In more detail, let <math>V</math> be a free module of finite rank over a commutative ring, and let <math> R, \bar{R} \in End(V \otimes V) </math> be invertible. Further, let there be invertible endomorphisms <math>M_\leftarrow, M_\rightarrow, M^\leftarrow, M^\rightarrow \in End(V) </math>; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices. |
||
The following notation is useful: for <math>n = dim(V)</math>, <math>R_{ab}^{cd}</math> refers to the element in row <math>n(c-1)+d</math> row and column <math>n(a-1) + b</math> |
The following notation is useful: for <math>n = dim(V)</math>, <math>R_{ab}^{cd}</math> refers to the element of '''''R''''' in row <math>n(c-1)+d</math> row and column <math>n(a-1) + b</math>. |
||
For an oriented knot or link <math>K</math>, REngine returns the product <math> \tau(K) </math>, which is computed as follows: |
For an oriented knot or link <math>K</math>, REngine returns the product <math> \tau(K) </math>, which is computed as follows: |
||
| Line 18: | Line 20: | ||
[[Image:REtref.png|right|frame|A trefoil knot]] |
|||
As an example, let ''K'' be the left-handed trefoil, as shown. Then |
|||
As an example, let ''K'' be the trefoil as shown, with the chosen axis upwards, and the strands going down through all the crossings. Then |
|||
:<math>\tau(K) = \sum {M_\leftarrow}_{ab} {M_\rightarrow}_{cd} R_{bc}^{ef} R_{ef}^{gh} R_{gh}^{ij} {M^\rightarrow}_{ai}{M^\leftarrow}_{jd}</math> |
|||
where the summation is carried out on all the indices ''a'' through ''i'', each ranging from 1 to n. |
|||
Determining that <math>\tau(K)</math> is actually an invariant is simply a matter of checking the equality of the outcomes of Reidemeister moves in various configurations and orientations, as well as a few 'topological' moves. Note that <code>REngine</code> does not perform any checks; the utility [[TestRMatrix]] does the tests required to determine regular isotopy. |
|||
<math>\tau(K) = \sum {M_\leftarrow}_{ab} </math> |
|||
Revision as of 16:07, 7 September 2005
KnotTheory` can compute knot and link invariants associated with matrix solutions of the Yang-Baxter equation, using the program REngine:
(For In[1] see Setup)
In more detail, let be a free module of finite rank over a commutative ring, and let be invertible. Further, let there be invertible endomorphisms ; these correspond to McupL, McupR, McapL, and McapR respectively. Fixing a basis of V, we can regard all of these endomorphisms as matrices.
The following notation is useful: for , refers to the element of R in row row and column .
For an oriented knot or link , REngine returns the product , which is computed as follows:
- Find a Morse link presentation of such that it is composed only of crossings of the
X[k, Over/Under, Down, Down]variety; this is accomplished by adding caps and cups where necessary. - Label the edges in between events in the Morse link presentation of .
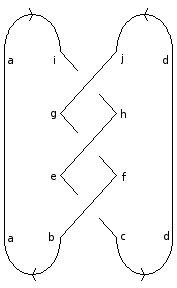
- Associate each event with one of the matrices as shown, with the indices given by the labelling:
- Define as the result of taking the product of the matrices associated with the elements of K, and summing over repeated indices; each sum runs from 1 to .
As an example, let K be the trefoil as shown, with the chosen axis upwards, and the strands going down through all the crossings. Then
where the summation is carried out on all the indices a through i, each ranging from 1 to n.
Determining that is actually an invariant is simply a matter of checking the equality of the outcomes of Reidemeister moves in various configurations and orientations, as well as a few 'topological' moves. Note that REngine does not perform any checks; the utility TestRMatrix does the tests required to determine regular isotopy.