Planar Diagrams: Difference between revisions
No edit summary |
No edit summary |
||
| (41 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
|||
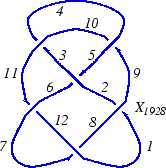
In the "Planar Diagrams" (<code>PD</code>) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols <math>X_{ijkl}</math> where <math>i</math>, <math>j</math>, <math>k</math> and <math>l</math> are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the <code>PD</code> presentation of the knot on the right is: |
|||
<!-- MATH |
|||
\begin{displaymath} |
|||
X_{1928} X_{3,10,4,11} X_{5362} X_{7,1,8,12} X_{9,4,10,5} X_{11,7,12,6}. |
|||
\end{displaymath} |
|||
--> |
|||
[[Image:PDNotation.gif|frame|center|The <code>PD</code> notation]] |
|||
<div align="CENTER">[[Image:img16.gif]] </div> |
|||
In the "Planar Diagrams" (<code>PD</code>) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols <math>X_{ijkl}</math> where <math>i</math>, <math>j</math>, <math>k</math> and <math>l</math> are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the <code>PD</code> presentation of the knot above is: |
|||
<center><math> |
|||
(This of course is the Miller Institute knot, the mirror image of the knot [http://www.math.toronto.edu/~drorbn/private/KAtlas/Knots/6.2.html [[Image:img17.gif]]].) |
|||
X_{1928} X_{3,10,4,11} X_{5362} X_{7,1,8,12} X_{9,4,10,5} X_{11,7,12,6}. |
|||
</math></center> |
|||
(This of course is the Miller Institute knot, the mirror image of the knot [[6_2]]) |
|||
<div align="CENTER"> |
|||
{{Startup Note}} |
|||
{| |
|||
|+ align="BOTTOM" |'''Figure 2:''' Our notation for planar diagrams |
|||
<!--$$?PD$$--> |
|||
|- |
|||
<!--Robot Land, no human edits to "END"--> |
|||
| align="center" | |
|||
{{HelpAndAbout| |
|||
[[Image:img18.gif]] |
|||
n = 2 | |
|||
|} |
|||
n1 = 3 | |
|||
in = <nowiki>PD</nowiki> | |
|||
out= <nowiki>PD[v1, v2, ...] represents a planar diagram whose vertices are v1, v2, .... PD also acts as a "type caster", so for example, PD[K] where K is a named knot (or link) returns the PD presentation of that knot.</nowiki> | |
|||
about= <nowiki>The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?X$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 4 | |
|||
in = <nowiki>X</nowiki> | |
|||
out= <nowiki>X[i,j,k,l] represents a crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counterclockwise through j, k and l. The (sometimes ambiguous) orientation of the upper strand is determined by the ordering of {j,l}.</nowiki>}} |
|||
<!--END--> |
|||
Thus, for example, let us compute the determinant of the above knot: |
|||
<!--$$K = PD[ |
|||
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], |
|||
X[7,1,8,12], X[9,4,10,5], X[11,7,12,6] |
|||
];$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{In| |
|||
n = 5 | |
|||
in = <nowiki>K = PD[ |
|||
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], |
|||
X[7,1,8,12], X[9,4,10,5], X[11,7,12,6] |
|||
];</nowiki>}} |
|||
<!--END--> |
|||
<!--$$Alexander[K][-1]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 6 | |
|||
in = <nowiki>Alexander[K][-1]</nowiki> | |
|||
out= <nowiki>-11</nowiki>}} |
|||
<!--END--> |
|||
<div id="Some further details"> |
|||
==== Some further details ==== |
|||
</div> |
|||
<!--$$?Xp$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 7 | |
|||
in = <nowiki>Xp</nowiki> | |
|||
out= <nowiki>Xp[i,j,k,l] represents a positive (right handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from l to j regardless of the ordering of {j,l}. Presently Xp is only lightly supported.</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?Xm$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 8 | |
|||
in = <nowiki>Xm</nowiki> | |
|||
out= <nowiki>Xm[i,j,k,l] represents a negative (left handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from j to l regardless of the ordering of {j,l}. Presently Xm is only lightly supported.</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?P$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 9 | |
|||
in = <nowiki>P</nowiki> | |
|||
out= <nowiki>P[i,j] represents a bivalent vertex whose adjacent edges are i and j (i.e., a "Point" between the segment i and the segment j). Presently P is only lightly supported.</nowiki>}} |
|||
<!--END--> |
|||
For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13: |
|||
<!--$$K1 = PD[ |
|||
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], |
|||
X[7,1,8,13], X[9,4,10,5], X[11,7,12,6], |
|||
P[12,13] |
|||
];$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{In| |
|||
n = 10 | |
|||
in = <nowiki>K1 = PD[ |
|||
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], |
|||
X[7,1,8,13], X[9,4,10,5], X[11,7,12,6], |
|||
P[12,13] |
|||
];</nowiki>}} |
|||
<!--END--> |
|||
At the moment, many of our routines do not know to ignore such "extra points". But some do: |
|||
<!--$$Jones[K][q] == Jones[K1][q]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 11 | |
|||
in = <nowiki>Jones[K][q] == Jones[K1][q]</nowiki> | |
|||
out= <nowiki>True</nowiki>}} |
|||
<!--END--> |
|||
<!--$$?Loop$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{HelpLine| |
|||
n = 12 | |
|||
in = <nowiki>Loop</nowiki> | |
|||
out= <nowiki>Loop[i] represents a crossingsless loop labeled i.</nowiki>}} |
|||
<!--END--> |
|||
Hence we can verify that the A2 invariant of the unknot is <math>q^{-2}+1+q^2</math>: |
|||
<!--$$A2Invariant[Loop[1]][q]$$--> |
|||
<!--Robot Land, no human edits to "END"--> |
|||
{{InOut| |
|||
n = 13 | |
|||
in = <nowiki>A2Invariant[Loop[1]][q]</nowiki> | |
|||
out= <nowiki> -2 2 |
|||
1 + q + q</nowiki>}} |
|||
<!--END--> |
|||
Latest revision as of 17:08, 21 February 2013
In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols where , , and are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot above is:
(This of course is the Miller Institute knot, the mirror image of the knot 6_2)
(For In[1] see Setup)
|
| ||||||||
| ||||
Thus, for example, let us compute the determinant of the above knot:
In[5]:=
|
K = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,12], X[9,4,10,5], X[11,7,12,6]
];
|
In[6]:=
|
Alexander[K][-1]
|
Out[6]=
|
-11
|
Some further details
| ||||
| ||||
| ||||
For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13:
In[10]:=
|
K1 = PD[
X[1,9,2,8], X[3,10,4,11], X[5,3,6,2],
X[7,1,8,13], X[9,4,10,5], X[11,7,12,6],
P[12,13]
];
|
At the moment, many of our routines do not know to ignore such "extra points". But some do:
In[11]:=
|
Jones[K][q] == Jones[K1][q]
|
Out[11]=
|
True
|
| ||||
Hence we can verify that the A2 invariant of the unknot is :
In[13]:=
|
A2Invariant[Loop[1]][q]
|
Out[13]=
|
-2 2
1 + q + q
|