Prime Links with a Non-Prime Component: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 44: | Line 44: | ||
Now, we can use the program [[SubLink.m|<code>SubLink</code>]] that determines the PD form of a knot (or a link) made up of the selected component(s) of a certain link: |
Now, we can use the program [[SubLink.m|<code>SubLink</code>]] that determines the PD form of a knot (or a link) made up of the selected component(s) of a certain link: |
||
<!--$$Import["http://katlas.org/ |
<!--$$Import["http://katlas.org/w/index.php?title=SubLink.m&action=raw"];$$--> |
||
<!--Robot Land, no human edits to "END"--> |
|||
{{In| |
|||
n = 4 | |
|||
in = <nowiki>Import["http://katlas.org/w/index.php?title=SubLink.m&action=raw"];</nowiki>}} |
|||
<!--END--> |
|||
Using <code>SubLink</code> and the Jones polynomials of the five composite knots mentioned above, we can find all links that have one of these as a component: |
Using <code>SubLink</code> and the Jones polynomials of the five composite knots mentioned above, we can find all links that have one of these as a component: |
||
Latest revision as of 14:00, 20 October 2013
Let us find all (prime!) links in the Knot Atlas that have a non-prime component. Since the links listed in the Knot Atlas have at most 11 crossings, such a component may only be the sum of exactly two knots chosen among the trefoil, the figure eight knot, and their mirror images. The figure eight knot's mirror image is itself so we have five possibilities. Computing the Jones polynomial of each, we get:
(For In[1] see Setup)
In[2]:=
|
K31 = Knot[3, 1]; K41 = Knot[4, 1];
|
In[3]:=
|
CompositeJones =
Jones[#][q] & /@ {ConnectedSum[K31, K31],
ConnectedSum[K31, Mirror[K31]],
ConnectedSum[Mirror[K31], Mirror[K31]], ConnectedSum[K31, K41],
ConnectedSum[Mirror[K31], K41]}
|
Out[3]=
|
-8 2 -6 2 2 -2 -3 -2 1 2 3
{q - -- + q - -- + -- + q , 3 - q + q - - - q + q - q ,
7 5 4 q
q q q
2 4 5 6 7 8
q + 2 q - 2 q + q - 2 q + q ,
-6 2 2 3 3 2
-1 - q + -- - -- + -- - -- + - + q,
5 4 3 2 q
q q q q
1 2 3 4 5 6
-1 + - + 2 q - 3 q + 3 q - 2 q + 2 q - q }
q
|
Now, we can use the program SubLink that determines the PD form of a knot (or a link) made up of the selected component(s) of a certain link:
In[4]:=
|
Import["http://katlas.org/w/index.php?title=SubLink.m&action=raw"];
|
Using SubLink and the Jones polynomials of the five composite knots mentioned above, we can find all links that have one of these as a component:
In[5]:=
|
NonPrimeComponentQ[L_] :=
Or @@ (MemberQ[CompositeJones, Jones[SubLink[L, #]][q]] & /@
Range[Length[Skeleton[L]]])
|
In[6]:=
|
Exceptions= Select[AllLinks[], NonPrimeComponentQ]
|
Out[6]=
|
{Link[10, Alternating, 38], Link[10, Alternating, 39],
Link[10, Alternating, 46], Link[10, NonAlternating, 35],
Link[10, NonAlternating, 36], Link[10, NonAlternating, 37],
Link[10, NonAlternating, 38], Link[10, NonAlternating, 39],
Link[11, Alternating, 91], Link[11, Alternating, 92],
Link[11, Alternating, 93], Link[11, Alternating, 95],
Link[11, Alternating, 121], Link[11, Alternating, 128],
Link[11, Alternating, 130], Link[11, NonAlternating, 110],
Link[11, NonAlternating, 111], Link[11, NonAlternating, 112],
Link[11, NonAlternating, 113], Link[11, NonAlternating, 114],
Link[11, NonAlternating, 115]}
|
Thus, there are 21 links in the Knot Atlas that have a non-prime component. The first eight of those are:
 L10a38 |
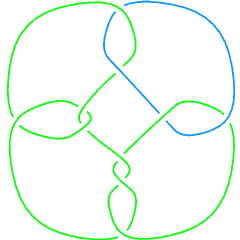 L10a39 |
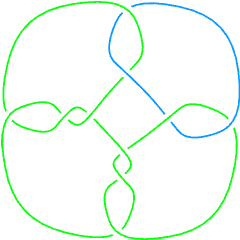 L10a46 |
 L10n35 |
 L10n36 |
 L10n37 |
 L10n38 |
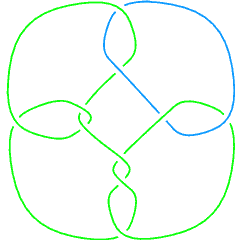 L10n39 |