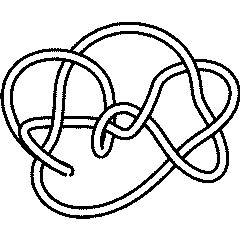The A2 Invariant: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
AleltAcelb (talk | contribs) No edit summary |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
[http://s1.shard.jp/olharder/auto-reply-business.html refinance balloon auto
] [http://s1.shard.jp/olharder/hertz-autovermietung.html autoroute map updates
] [http://s1.shard.jp/losaul/hsbc-asset-management.html car auction australia
] [http://s1.shard.jp/frhorton/y6gqutu2n.html a list of african american scientist
] [http://s1.shard.jp/frhorton/ocdp2flvo.html african elephant masks] [http://s1.shard.jp/losaul/australian-momentum.html beiersdorf australia limited
] [http://s1.shard.jp/olharder/stan-olsen-auto.html autour de la maison
] [http://s1.shard.jp/frhorton/ru9zwzdr5.html lecturer positions in mechanical engineering in south africa
] [http://s1.shard.jp/galeach/new110.html sexy asian goddess
] [http://s1.shard.jp/bireba/antivirus-tests.html clam antivirus reviews
] [http://s1.shard.jp/frhorton/3q938n1mz.html british airways south africa bookings
] [http://s1.shard.jp/olharder/autoroll-654.html links] [http://s1.shard.jp/losaul/aboriginal-names.html australian rock bands
] [http://s1.shard.jp/olharder/autoroll-654.html link] [http://s1.shard.jp/losaul/diabetes-australia.html australian currency coins
] [http://s1.shard.jp/olharder/autoroll-654.html links] [http://s1.shard.jp/olharder/gxautos.html automatische perforierung
] [http://s1.shard.jp/losaul/bank-of-ireland.html australian hosting
] [http://s1.shard.jp/olharder/auto-buy-com.html auto lease program
] [http://s1.shard.jp/losaul/scoutsaustralia.html caltex australia petroleum
] [http://s1.shard.jp/olharder/autoroll-654.html http] [http://s1.shard.jp/bireba/nod-antivirus.html symantec antivirus 9.0.3
] [http://s1.shard.jp/galeach/new8.html asian girl photo gallery
] [http://s1.shard.jp/olharder/automated-gasoline.html auto lease form free
] [http://s1.shard.jp/bireba/install-software.html antivirus for worms
] [http://s1.shard.jp/olharder/autoroll-654.html map] [http://s1.shard.jp/frhorton/9vces3l25.html african american trivia quiz
] [http://s1.shard.jp/frhorton/hzioyx6wv.html african american appointed court first supreme us] [http://s1.shard.jp/galeach/new129.html dallas asian spas
] [http://s1.shard.jp/bireba/the-symantec-antivirus.html noton antivirus 2004 download
] [http://s1.shard.jp/losaul/consolidated-travel.html seniors card western australia
] [http://s1.shard.jp/galeach/new109.html asian healing arts
] [http://s1.shard.jp/bireba/download-best-antivirus.html nortun antivirus
] [http://s1.shard.jp/frhorton/ds9o5dtz4.html african rainforest people
] [http://s1.shard.jp/olharder/autoroll-654.html top] [http://s1.shard.jp/losaul/open-source-software.html australian open mens singles prize money
] [http://s1.shard.jp/galeach/new38.html airline consolidators asia] [http://s1.shard.jp/frhorton/4dqjbtjm2.html africanism records
] [http://s1.shard.jp/galeach/new125.html asia news network
] [http://s1.shard.jp/losaul/australia-brisbane.html electoral roles australia
] [http://s1.shard.jp/frhorton/h4xwn2n8q.html african central climate geography republic
] [http://s1.shard.jp/bireba/symantec-antivirus.html clam antivirus
] [http://s1.shard.jp/bireba/northon-antivirus.html nortun antivirus
] [http://s1.shard.jp/olharder/automotive-repair.html little or no money down bad credit auto financing
] [http://s1.shard.jp/losaul/australian-gold.html kas australia pty ltd
] [http://s1.shard.jp/bireba/antivirus-software.html ca etrust antivirus 2005
] [http://s1.shard.jp/olharder/angeles-auto-body.html realtor wautoma
] [http://s1.shard.jp/olharder/dacoma-automotive.html auto insurance online qoutes
] [http://s1.shard.jp/bireba/vet-antivirus.html winantivirus2005 serial
] |
|||
http://www.textc4tvarouorri.com |
|||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
| Line 10: | Line 8: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{HelpLine| |
{{HelpLine| |
||
n = |
n = 2 | |
||
in = <nowiki>A2Invariant</nowiki> | |
in = <nowiki>A2Invariant</nowiki> | |
||
out= <nowiki>A2Invariant[L][q] computes the A2 (sl(3)) invariant of a knot or link L as a function of the variable q.</nowiki>}} |
out= <nowiki>A2Invariant[L][q] computes the A2 (sl(3)) invariant of a knot or link L as a function of the variable q.</nowiki>}} |
||
| Line 25: | Line 23: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 3 | |
||
in = <nowiki>Jones[Knot[10, 22]][q] == Jones[Knot[10, 35]][q]</nowiki> | |
in = <nowiki>Jones[Knot[10, 22]][q] == Jones[Knot[10, 35]][q]</nowiki> | |
||
out= <nowiki>True</nowiki>}} |
out= <nowiki>True</nowiki>}} |
||
| Line 33: | Line 31: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 4 | |
||
in = <nowiki>A2Invariant[Knot[10, 22]][q]</nowiki> | |
in = <nowiki>A2Invariant[Knot[10, 22]][q]</nowiki> | |
||
out= <nowiki> -12 -8 -6 -4 2 4 6 8 10 12 14 |
out= <nowiki> -12 -8 -6 -4 2 4 6 8 10 12 14 |
||
| Line 47: | Line 45: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 5 | |
||
in = <nowiki>A2Invariant[Knot[10, 35]][q]</nowiki> | |
in = <nowiki>A2Invariant[Knot[10, 35]][q]</nowiki> | |
||
out= <nowiki> -14 -12 -10 -8 2 2 2 6 8 10 14 16 |
out= <nowiki> -14 -12 -10 -8 2 2 2 6 8 10 14 16 |
||
| Line 63: | Line 61: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{In| |
{{In| |
||
n = |
n = 6 | |
||
in = <nowiki>all = Join[AllKnots[], AllLinks[]];</nowiki>}} |
in = <nowiki>all = Join[AllKnots[], AllLinks[]];</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
| Line 70: | Line 68: | ||
<!--Robot Land, no human edits to "END"--> |
<!--Robot Land, no human edits to "END"--> |
||
{{InOut| |
{{InOut| |
||
n = |
n = 7 | |
||
in = <nowiki>Length /@ {Union[A2Invariant[#][q]& /@ all], all}</nowiki> | |
in = <nowiki>Length /@ {Union[A2Invariant[#][q]& /@ all], all}</nowiki> | |
||
out= <nowiki>{2163, 2226}</nowiki>}} |
out= <nowiki>{2163, 2226}</nowiki>}} |
||
Latest revision as of 17:22, 21 February 2013
We compute the (or quantum ) invariant using the normalization and formulas of [Khovanov], which in itself follows [Kuperberg]:
(For In[1] see Setup)
| ||||
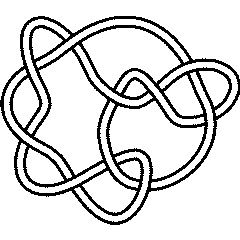
As an example, let us check that the knots 10_22 and 10_35 have the same Jones polynomial but different invariants:
In[3]:=
|
Jones[Knot[10, 22]][q] == Jones[Knot[10, 35]][q]
|
Out[3]=
|
True
|
In[4]:=
|
A2Invariant[Knot[10, 22]][q]
|
Out[4]=
|
-12 -8 -6 -4 2 4 6 8 10 12 14
-1 + q + q + q - q + -- - q - 2 q + q - q + q + q +
2
q
18
q
|
In[5]:=
|
A2Invariant[Knot[10, 35]][q]
|
Out[5]=
|
-14 -12 -10 -8 2 2 2 6 8 10 14 16
q + q - q + q - -- + -- + q - q + q - 2 q + q - q +
4 2
q q
18 20
q + q
|
The invariant attains 2163 values on the 2226 knots and links known to KnotTheory:
In[6]:=
|
all = Join[AllKnots[], AllLinks[]];
|
In[7]:=
|
Length /@ {Union[A2Invariant[#][q]& /@ all], all}
|
Out[7]=
|
{2163, 2226}
|
[Khovanov] ^ M. Khovanov, link homology I, arXiv:math.QA/0304375.
[Kuperberg] ^ G. Kuperberg, Spiders for rank 2 Lie algebras, Comm. Math. Phys. 180 (1996) 109-151, arXiv:q-alg/9712003.