File:Borromean-chain-mail.gif: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
(updating with info) |
(cross-ref) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
The "Borromean chain mail" knot -- two rings (here the red and blue) in a Borromean rings configuration (or L6a4 knot) with each of two other rings, such that no two rings are directly linked. The whole is [[L10n107]]. |
The "Borromean chain mail" knot -- two rings (here the red and blue) in a Borromean rings configuration (or [[L6a4]] knot) with each of two other rings, such that no two rings are directly linked. The whole is [[L10n107]]. Cutting the either the red or the blue rings frees the other three (leaving three separate disconnected loops), but cutting the yellow or green rings doesn't (so this is not a [[Brunnian link]].) |
||
For an indefinitely-extended Borromean chainmail pattern, see [[:Image:Borromean-chainmail-tile.gif]] . |
|||
Self-made. |
Self-made. |
||
Latest revision as of 18:23, 3 May 2006
The "Borromean chain mail" knot -- two rings (here the red and blue) in a Borromean rings configuration (or L6a4 knot) with each of two other rings, such that no two rings are directly linked. The whole is L10n107. Cutting the either the red or the blue rings frees the other three (leaving three separate disconnected loops), but cutting the yellow or green rings doesn't (so this is not a Brunnian link.)
For an indefinitely-extended Borromean chainmail pattern, see Image:Borromean-chainmail-tile.gif .
Self-made.
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 23:22, 28 March 2006 | 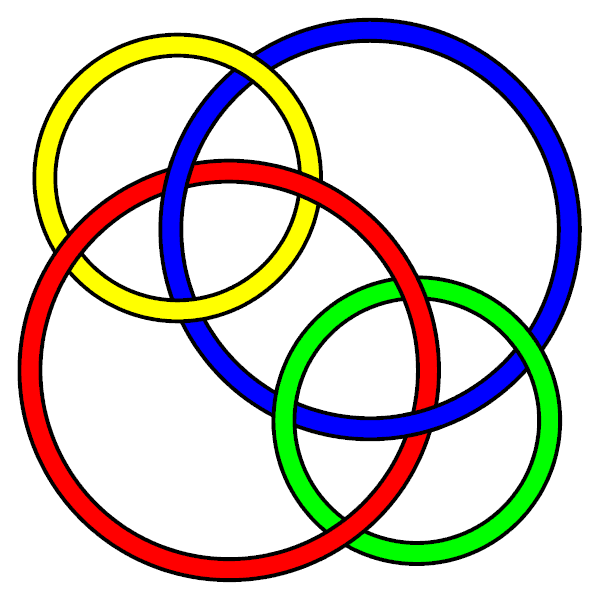 | 600 × 600 (19 KB) | AnonMoos (talk | contribs) | better version of pic |
| 15:45, 27 March 2006 | 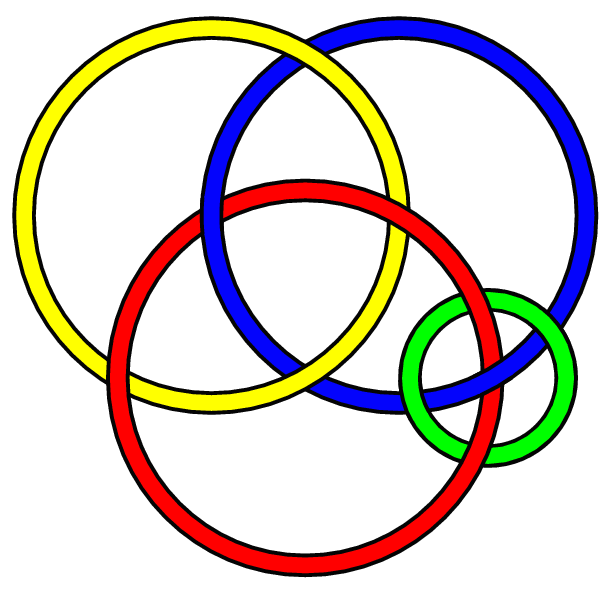 | 611 × 591 (25 KB) | AnonMoos (talk | contribs) | The "Borromean chain mail" knot -- two rings (here the red and blue) in a Borromean rings configuration (or L6a4 knot) with each of two other rings, such that no two rings are directly linked. Having difficulty determining which knot number is valid for |
You cannot overwrite this file.
File usage
The following 4 pages use this file: