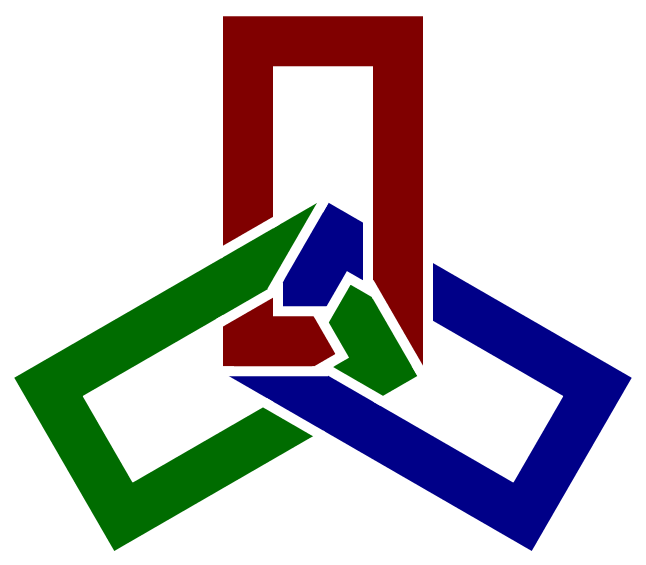
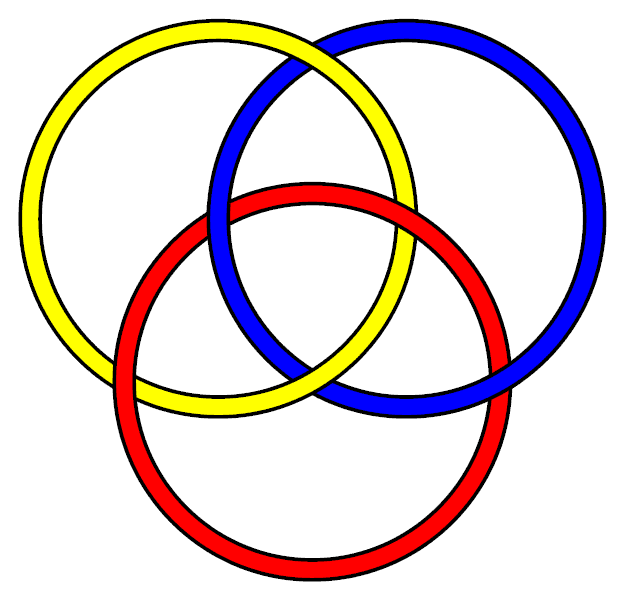L6a4

L6a3

L6a5

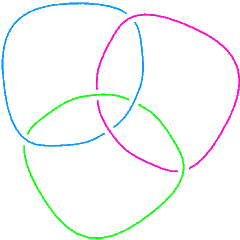(Knotscape image)

See the full Thistlethwaite Link Table (up to 11 crossings). Visit L6a4 at Knotilus!

The link L6a4 is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6^3_2} in the Rolfsen table of links. It is also known as the "Borromean Link" or the "Borromean Rings". A Brunnian link - no two loops are linked directly together, but all three rings are collectively interlinked [9]. Visit Peter Cromwell's page on the Borromean Rings.

Classic-type Borromean rings diagram with color-coded circles	Medieval-style representation of the Borromean rings, used as an emblem of Lorenzo de Medici in San Pancrazio, Florence[1]	A kolam with 3 cycles [2]	A version of the coat of arms of the Borromeo family
The Colombo Mall in Lisboa [3]	The Borromean rings as a symbol of the Christian Trinity (based on a 13th-century French manuscript)	One version of the Germanic "Valknut"	Coat of arms of Hallsberg, Sweden, with padlocks in Borromean configuration
A "Borromean" bathroom tile (the Diane de Poitiers three interlaced crescents emblem) [4]	Rectangles in three dimensions	A Borromean link at the Fields Institute [5]	Basic black-and-white depiction with minimal central overlap
3D depiction	3D depiction which purports to show simple circular toruses interlinked as Borromean rings (something which is actually geometrically impossible).	Asymmetrical depiction	Interlaced rectangles (Miguni, Fukui, Japan).
Borromean rings interlinked with cross as Christian symbol.	A practical application of the Borromean rings (Ballard Locks, Seattle)	Borromean paper clips [6]	A Borromean link by Dylan Thurston [7]
A Borromean rattle by Sassy [8]

Link Presentations

[edit Notes on L6a4's Link Presentations]

Planar diagram presentation	X6172 X12,8,9,7 X4,12,1,11 X10,5,11,6 X8453 X2,9,3,10
Gauss code	{1, -6, 5, -3}, {4, -1, 2, -5}, {6, -4, 3, -2}

A Braid Representative
A Morse Link Presentation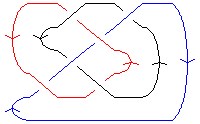

Polynomial invariants

Multivariable Alexander Polynomial (in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle w} , ...)	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{(u-1) (v-1) (w-1)}{\sqrt{u} \sqrt{v} \sqrt{w}}} (db)
Jones polynomial	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -q^3- q^{-3} +3 q^2+3 q^{-2} -2 q-2 q^{-1} +4} (db)
Signature	0 (db)
HOMFLY-PT polynomial	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -a^2 z^2-z^2 a^{-2} +a^2 z^{-2} + a^{-2} z^{-2} +z^4+2 z^2-2 z^{-2} } (db)
Kauffman polynomial	Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^3 z^3+z^3 a^{-3} +3 a^2 z^4+3 z^4 a^{-2} -4 a^2 z^2-4 z^2 a^{-2} +a^2 z^{-2} + a^{-2} z^{-2} +2 a z^5+2 z^5 a^{-1} -a z^3-z^3 a^{-1} -2 a z^{-1} -2 a^{-1} z^{-1} +6 z^4-8 z^2+2 z^{-2} +1} (db)

Khovanov Homology

The coefficients of the monomials Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t^rq^j} are shown, along with their alternating sums Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} (fixed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , alternation over Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} ).

\   r    \    j   \ -3 -2 -1 0 1 2 3 χ 7             1 -1 5           2   2 3           1   1 1       4 2     2 -1     2 4       2 -3   1           1 -5   2           2 -7 1             -1

Integral Khovanov Homology (db, data source)

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \dim{\mathcal G}_{2r+i}\operatorname{KH}^r_{\mathbb Z}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=-1} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1} $r=-3$ Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=-2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{2}\oplus{\mathbb Z}_2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=-1} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}_2^{2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{4}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{4}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=1} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}\oplus{\mathbb Z}_2^{2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}^{2}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=3} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}_2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mathbb Z}}

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

Modifying This Page

Read me first: Modifying Knot Pages See/edit the Link Page master template (intermediate). See/edit the Link_Splice_Base (expert). Back to the top.

L6a3 L6a5