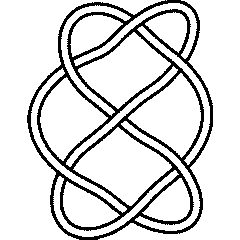Torus Knot Splice Base: Difference between revisions

From Knot Atlas
Jump to navigationJump to search
No edit summary
No edit summary
Line 7: Line 7:
{{TorusKnotsNavigation|<*PreviousKnot*>|<*NextKnot*>}}
{{TorusKnotsNavigation|<*PreviousKnot*>|<*NextKnot*>}}


{| style="width: 20%; float: right;" |
{{:Further <*ThisKnot*> views}}
|
<center>
[[Image:{{Data:7_5/Previous Knot}}.gif|60px]]


[[{{Data:7_5/Previous Knot}}]]
[[Planar Diagrams|Planar Diagram]]: <* PD[K] *>
</center>
|
<center>
[[Image:{{Data:7_5/Next Knot}}.gif|60px]]


[[{{Data:7_5/Next Knot}}]]
<table border=0><tr align=center>
<td>
<a href="../Manual/TubePlot.html"><img src="<*m*>.<*n*>_240.jpg"
border=0 alt="T(<*m*>,<*n*>)"><br><font size=-2>TubePlot</font></a>
</td>
<td>
<h1>&nbsp;&nbsp; The <*m(n-1)*>-Crossing Torus Knot T(<*m*>,<*n*>)</h1>
<*Include["$knotaka.html"]*>
<p>Visit <a class=external
href="<*KnotilusURL[K=TorusKnot[m, n]]*>">T(<*m*>,<*n*>)'s
page</a> at <a class=external
href="http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/html/start.html">Kno
tilus</a>!
<p><a href="../Manual/Acknowledgement.html">Acknowledgement</a>
</td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/GaussCode.html">Gauss Code</a>: </td>
<td><em><*List @@ GaussCode[K]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/BR.html">Braid Representative</a>: </td>
<td>&nbsp;&nbsp;&nbsp;</td>
<td>
<* BraidPlot[CollapseBraid[BR[K]], Mode -> "HTML"] *>
</td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/AlexanderConway.html">Alexander Polynomial</a>:
</td>
<td><em><*PolyPrint[alex = Alexander[K][t], t]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/AlexanderConway.html">Conway Polynomial</a>: </td>
<td><em><*PolyPrint[Conway[K][z], z]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td>Other knots with the same <a
href="../Manual/AlexanderConway.html">Alexander/Conway Polynomial</a>:
</td>
<td><em>{<*
others =
DeleteCases[Select[AllKnots[], (alex === Alexander[#][t])&],
Knot[n,Type,k]];
If[others === {}, "",
StringJoin[(ToString[#, FormatType -> HTMLForm]<>", ")& /@ others]
]
*>...}</em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td>
<a href="../Manual/DetAndSignature.html">Determinant and Signature</a>:
</td>
<td><em><*{KnotDet[K], s=KnotSignature[K]}*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/Jones.html">Jones Polynomial</a>:
</td>
<td><em><*PolyPrint[J = Jones[K][q], q]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td>Other knots (up to mirrors) with the same <a
href="../Manual/Jones.html">Jones Polynomial</a>:
</td>
<td><em>{<*
others =
DeleteCases[Select[AllKnots[],
(J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&
], Knot[n,Type,k]];
If[others === {}, "",
StringJoin[(ToString[#, FormatType -> HTMLForm]<>", ")& /@ others]
]
*>...}</em></td>
</tr></table>

<* If[Crossings[K]<=18, Include["ColouredJones.mhtml"] ,""] *>

<p><table><tr align=left valign=top>
<td><a href="../Manual/A2Invariant.html">A2 (sl(3)) Invariant</a>:
</td>
<td><em><*PolyPrint[A2Invariant[K][q], q]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/Kauffman.html">Kauffman Polynomial</a>:
</td>
<td><em><*PolyPrint[Kauffman[K][a, z], {a, z}]*></em></td>
</tr></table>

<p><table><tr align=left valign=top>
<td><a href="../Manual/Vassiliev.html">V<sub>2</sub> and
V<sub>3</sub>, the type 2 and 3 Vassiliev invariants</a>: </td>
<td><em><* {Vassiliev[2][K], Vassiliev[3][K]} *></em></td>
</tr></table>

<p><a href="../Manual/KhovanovHomology.html">Khovanov Homology</a>.
The coefficients of the monomials <em>t<sup>r</sup>q<sup>j</sup></em>
are shown, along with their alternating sums &chi; (fixed <em>j</em>,
alternation over <em>r</em>).
The squares with <font class=HLYellow>yellow</font> highlighting
are those on the "critical diagonals", where <em>j-2r=s+1</em> or
<em>j-2r=s+1</em>, where <em>s=<*s*></em> is the signature of
T(<*m*>,<*n*>). Nonzero entries off the critical diagonals (if
any exist) are highlighted in <font class=HLRed>red</font>.
<br><center>
<*TabularKh[Kh[K][q, t], s+{1,-1}]*>
</center>
</center>
|}


{{Knot Site Links|n=7|k=5}}
<* ComputerTalkHeader *>

<*GraphicsBox["`1`.`2`_240.jpg", "TubePlot[TorusKnot[`1`, `2`]]", m, n]*>
<*InOut["Crossings[``]", K]*>
<*InOut["PD[``]", K]*>
<*InOut["GaussCode[``]", K]*>
<*InOut["BR[``]", K]*>
<*InOut["alex = Alexander[``][t]", K]*>
<*InOut["Conway[``][z]", K]*>
<*InOut["Select[AllKnots[], (alex === Alexander[#][t])&]"]*>
<*InOut["{KnotDet[`1`], KnotSignature[`1`]}", K]*>
<*InOut["J=Jones[``][q]", K]*>
<*InOut[
"Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]"
]*>
<* If[Crossings[K]<=18, Include["ColouredJonesM.mhtml"] ,""] *>
<*InOut["A2Invariant[``][q]", K]*>
<*InOut["Kauffman[``][a, z]", K]*>
<*InOut["{Vassiliev[2][`1`], Vassiliev[3][`1`]}", K ]*>
<*InOut["Kh[``][q, t]", K]*>

</table>

<p><hr><p>

<table valign=center width=100% border=0><tr>
<td align=left>
<a href="/~drorbn/">Dror Bar-Natan</a>:
<a href="../index.html">The Knot Atlas</a>:
<a href="index.html">Torus Knots</a>:
<a href="#top">The Torus Knot T(<*m*>,<*n*>)</a>
</td>
<td align=right>
<table border=0><tr>
<td align=center>
<a href="<*prevm*>.<*prevn*>.html"><img border=0
width=120 height=120 src="<*prevm*>.<*prevn*>_120.jpg"
alt="T(<*prevm*>,<*prevn*>)"><br>T(<*prevm*>,<*prevn*>)</a>
</td><td align=center>
<a href="<*nextm*>.<*nextn*>.html"><img border=0
width=120 height=120 src="<*nextm*>.<*nextn*>_120.jpg"
alt="T(<*nextm*>,<*nextn*>)"><br>T(<*nextm*>,<*nextn*>)</a>
</td>
</tr></table>
</td>
</tr></table>


{{Knot Presentations|name=7_5}}
</body>
===[[Three Dimensional Invariants|Three dimensional invariants]]===
</html>
{|
| Symmetry type
| {{Data:7_5/Symmetry Type}}
|-
| Unknotting number
| {{Data:7_5/Unknotting Number}}
|-
| 3-genus
| {{Data:7_5/3-Genus}}
|-
| Bridge index (super bridge index)
| {{Data:7_5/Bridge Index}} ({{Data:7_5/Super Bridge Index}})
|-
| Nakanishi index
| {{Data:7_5/Nakanishi Index}}
|}
{{Polynomial Invariants|name=7_5}}
{{Vassiliev Invariants|name=7_5}}
{{Khovanov Invariants|name=7_5}}
{{Quantum Invariants|name=7_5}}

Revision as of 21:00, 25 August 2005


Previous: [[<*PreviousKnot*>]]; Next: [[<*NextKnot*>]]

7 4.gif

7_4

7 6.gif

7_6

Visit Torus Knot Splice Base's page at the Knot Server (KnotPlot driven, includes 3D interactive images!)

Visit [{{{KnotilusURL}}} Torus Knot Splice Base's page] at Knotilus!

Visit Torus Knot Splice Base's page at the original Knot Atlas!

Knot presentations

Planar diagram presentation Data:Torus Knot Splice Base/PD Presentation
Gauss code Data:Torus Knot Splice Base/Gauss Code
Dowker-Thistlethwaite code Data:Torus Knot Splice Base/DT Code
Conway Notation Data:Torus Knot Splice Base/Conway Notation

Three dimensional invariants

Symmetry type Reversible
Unknotting number 2
3-genus 2
Bridge index (super bridge index) 2 (4)
Nakanishi index 1

Polynomial invariants

Alexander polynomial Data:Torus Knot Splice Base/Alexander Polynomial
Conway polynomial Data:Torus Knot Splice Base/Conway Polynomial
2nd Alexander ideal (db, data sources) Data:Torus Knot Splice Base/2nd AlexanderIdeal
Determinant and Signature { Data:Torus Knot Splice Base/Determinant, Data:Torus Knot Splice Base/Signature }
Jones polynomial Data:Torus Knot Splice Base/Jones Polynomial
HOMFLY-PT polynomial (db, data sources) Data:Torus Knot Splice Base/HOMFLYPT Polynomial
Kauffman polynomial (db, data sources) Data:Torus Knot Splice Base/Kauffman Polynomial
The A2 invariant Data:Torus Knot Splice Base/QuantumInvariant/A2/1,0
The G2 invariant Data:Torus Knot Splice Base/QuantumInvariant/G2/1,0

Vassiliev invariants

V2 and V3: (Data:Torus Knot Splice Base/V 2, Data:Torus Knot Splice Base/V 3)
V2,1 through V6,9:
V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9
Data:Torus Knot Splice Base/V 2,1 Data:Torus Knot Splice Base/V 3,1 Data:Torus Knot Splice Base/V 4,1 Data:Torus Knot Splice Base/V 4,2 Data:Torus Knot Splice Base/V 4,3 Data:Torus Knot Splice Base/V 5,1 Data:Torus Knot Splice Base/V 5,2 Data:Torus Knot Splice Base/V 5,3 Data:Torus Knot Splice Base/V 5,4 Data:Torus Knot Splice Base/V 6,1 Data:Torus Knot Splice Base/V 6,2 Data:Torus Knot Splice Base/V 6,3 Data:Torus Knot Splice Base/V 6,4 Data:Torus Knot Splice Base/V 6,5 Data:Torus Knot Splice Base/V 6,6 Data:Torus Knot Splice Base/V 6,7 Data:Torus Knot Splice Base/V 6,8 Data:Torus Knot Splice Base/V 6,9

V2,1 through V6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V2 and V3.

Template:Khovanov Invariants Template:Quantum Invariants

Retrieved from "https://katlas.org/index.php?title=Torus_Knot_Splice_Base&oldid=1648"