"Rubberband" Brunnian Links

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

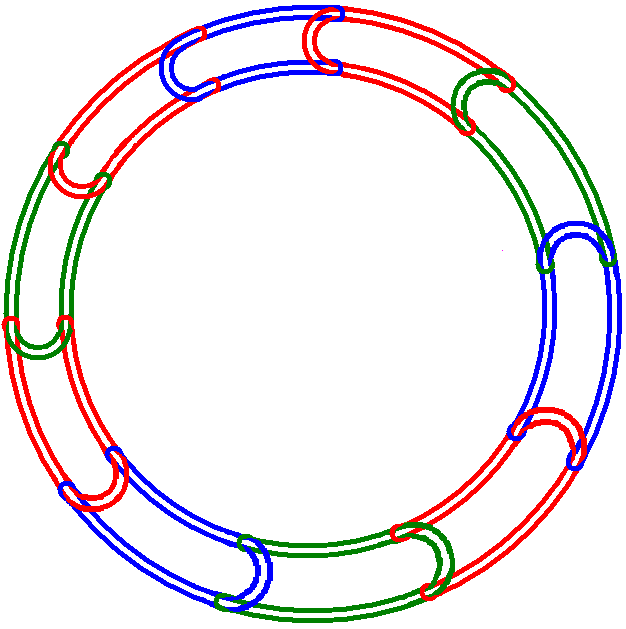
A "Rubberband" Brunnian link is obtained by connecting unknots in a closed chain as illustrated in the diagram of the 10-component link, where the last knot gets connected to the first one.

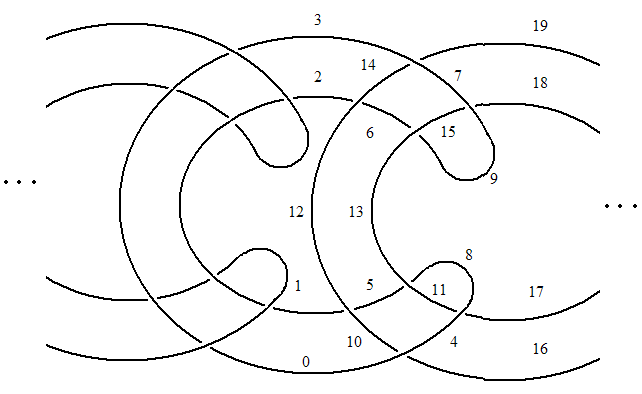
If we number the strands in one section of the link as shown and proceed with numbering each following section in the same manner, we can get its PD form. The PD of any "Rubberband" link can be generated in this way by varying the desired number of components:

(For In[1] see Setup)

In[1]:=

K0 = PD[X[1, 10, 5, 12], X[2, 12, 6, 14], X[5, 11, 8, 13], X[6, 13, 9, 15], X[10, 0, 16, 4], X[11, 4, 17, 8], X[14, 7, 19, 3], X[15, 9, 18, 7]];

In[2]:=

RubberBandBrunnian[n_] := Join @@ Table[K0 /. j_Integer :> j + 16 k, {k, 0, n - 1}] /. {16 n -> 0, 16 n + 1 -> 1, 16 n + 2 -> 2, 16 n + 3 -> 3}

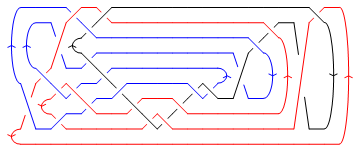
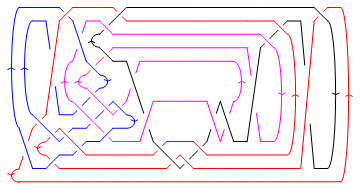
For instance, let us draw the links with three, four, and five components and compute their Jones polynomials:

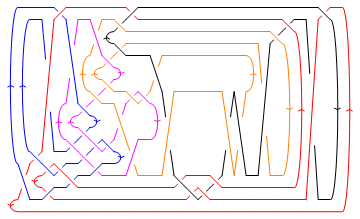
In[4]:=	DrawMorseLink[RBB3=RubberBandBrunnian[3]]
Out[4]=	-Graphics-

In[5]:=	Jones[RBB3][q]
Out[5]=	2 3 4 5 7 8 9 10 -q + 5 q - 11 q + 14 q - 10 q + 11 q - 18 q + 24 q - 18 q + 11 13 14 15 16 17 11 q - 10 q + 14 q - 11 q + 5 q - q

In[7]:=	DrawMorseLink[RBB4=RubberBandBrunnian[4]]
Out[7]=	-Graphics-

In[8]:=	Jones[RBB4][q]
Out[8]=	3/2 5/2 7/2 9/2 11/2 13/2 15/2 -q + 7 q - 24 q + 49 q - 56 q + 18 q + 51 q - 17/2 19/2 21/2 23/2 25/2 27/2 111 q + 131 q - 100 q + 32 q + 32 q - 100 q + 29/2 31/2 33/2 35/2 37/2 39/2 131 q - 111 q + 51 q + 18 q - 56 q + 49 q - 41/2 43/2 45/2 24 q + 7 q - q

In[10]:=	DrawMorseLink[RBB5=RubberBandBrunnian[5]]
Out[10]=	-Graphics-

In[11]:=	Jones[RBB5][q]
Out[11]=	2 3 4 5 6 7 8 9 -q + 9 q - 40 q + 110 q - 189 q + 167 q + 57 q - 414 q + 10 11 12 13 14 15 16 660 q - 581 q + 189 q + 305 q - 672 q + 816 q - 672 q + 17 18 19 20 21 22 23 305 q + 189 q - 581 q + 660 q - 414 q + 57 q + 167 q - 24 25 26 27 28 189 q + 110 q - 40 q + 9 q - q

We can also check that when one component is removed the remaining link is trivial:

In[12]:=

SubLink[pd_PD, js_List] := Module[ {k, t0, t, t1, t2, S, P}, t0 = Flatten[List @@@ Skeleton[pd][[js]]]; t = pd /. x_X :> Select[x, MemberQ[t0, #] &]; t = DeleteCases[t, X[]]; k = 1; While[ k <= Length[t], If[ Length[t[[k]]] < 4, t = Delete[t, k] /. (Rule @@ t[[k]]), ++k]; ]; t1 = List @@ Union @@ t; t2 = Thread[(t1) -> Range[Length[t1]]]; S = t /. t2; P = If[S != PD[] && Length[S] >= 3, S, PD[Knot[0, 1]], S] ]; SubLink[pd_PD, j_] := SubLink[pd, {j}]; SubLink[L_, js_] := SubLink[PD[L], js];

In[13]:=

S = SubLink[RubberBandBrunnian[5], {1, 2, 3, 4}];

In[14]:=	J=Factor[Jones[S][q]]
Out[14]=	6 3 -(q (1 + q) )

Brunnian Braids

Similarly, in the case of Brunnian braids, removing one strand gives us a trivial braid. We can verify that using the following two programs. The first one constructs a Brunnian braid while the second one removes a selected strand:

In[15]:=

BR /: Inverse[BR[n_, l_List]] := BR[n, -Reverse[l]]; BR /: BR[n1_, l1_] ** BR[n2_, l2_] := BR[Max[n1, n2], Join[l1, l2]]; BrunnianBraid[2] = BR[2, {1, 1}]; BrunnianBraid[n_] /; n > 2 := Module[ {b0}, b0 = BrunnianBraid[n - 1]; ((b0 ** BR[n, {n - 1, n - 1}]) ** Inverse[b0]) ** BR[n, {1 - n, 1 - n}] ]

In[16]:=

DeleteStrand[k_, BR[n_, l_List]] := BR[n - 1, DeleteStrand[k, l]]; DeleteStrand[k_, {}] = {}; DeleteStrand[k_, {j1_, js___}] := Which[ k < Abs[j1], {j1 - Sign[j1]}~Join~DeleteStrand[k, {js}], k == Abs[j1], DeleteStrand[k + 1, {js}], k == Abs[j1] + 1, DeleteStrand[k - 1, {js}], k > Abs[j1] + 1, {j1}~Join~DeleteStrand[k, {js}] ]

Testing for the Brunnian braid with four strands, we get:

In[18]:=	(b = BrunnianBraid[4]) // BraidPlot
Out[18]=	-Graphics-

In[19]:=	Jones[b][q]
Out[19]=	-(11/2) 4 6 5 5 1 3/2 -q + ---- - ---- + ---- - ---- - ------- - Sqrt[q] - 5 q + 9/2 7/2 5/2 3/2 Sqrt[q] q q q q 5/2 7/2 9/2 11/2 5 q - 6 q + 4 q - q

In[21]:=	(bb = DeleteStrand[4, b]) // BraidPlot
Out[21]=	-Graphics-

In[22]:=	Jones[#][q] & /@ {bb, BR[3, {}]}
Out[22]=	1 1 {2 + - + q, 2 + - + q} q q