Arc Presentations

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

An Arc Presentation $A$ of a knot $K$ (in "grid form", to be precise) is a planar (toroidal, to be precise) picture of the knot in which all arcs are either horizontal or vertical, in which the vertical arcs are alway "above" the horizontal arcs, and in which no two horizontal arcs have the same $y$-coordinate and no two vertical arcs have the same $x$-coordinate (read more at [1]). Without loss of generality, the $x$-coordinates of the vertical arcs in $A$ are the integers $1$ through $n$ for some $n$, and the $y$-coordinates of the horizontal arcs in $A$ are (also!) the integers $1$ through $n$.

KnotTheory` knows about arc presentations:

(For In[1] see Setup)

In[1]:= ?ArcPresentation ArcPresentation[{a1,b1}, {a2, b2}, ..., {an,bn}] is an arc presentation of a knot (as often used in the realm of Heegaard-Floer homologies), where the horizontal arc at row i connects column ai to column bi. ArcPresentation[K] returns an arc presentation of the knot K. ArcPresentation[K, Reduce -> r] attemps at most r reduction steps (using a naive reduction algorithm) following a naive creation of some arc presentation for K.

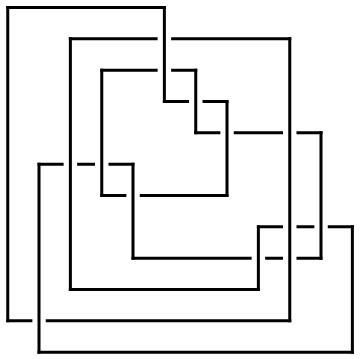
In[2]:=	ap = ArcPresentation["K11n11"]
Out[2]=	ArcPresentation[{12, 2}, {1, 10}, {3, 9}, {5, 11}, {9, 12}, {4, 8}, {2, 5}, {11, 7}, {8, 6}, {7, 4}, {10, 3}, {6, 1}]

In[4]:=	Draw[ap]
Out[4]=	-Graphics-

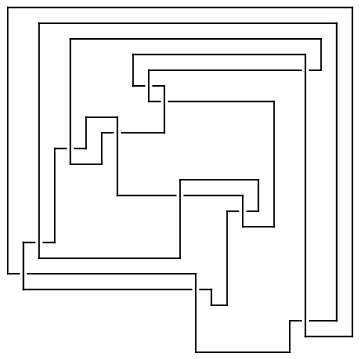
In[5]:=	ap0 = ArcPresentation["K11n11", Reduce -> 0]
Out[5]=	ArcPresentation[{13, 19}, {20, 23}, {19, 22}, {15, 14}, {14, 2}, {1, 13}, {3, 12}, {2, 4}, {16, 18}, {17, 15}, {8, 16}, {12, 17}, {5, 7}, {4, 6}, {7, 11}, {6, 8}, {18, 10}, {11, 9}, {10, 21}, {9, 20}, {21, 5}, {22, 3}, {23, 1}]

In[6]:= ?Draw Draw[ap] draws the Arc Presentation ap. Draw[ap, OverlayMatrix -> M] overlays the matrix M on top of that draw.

In[8]:=	Draw[ap0]
Out[8]=	-Graphics-

In[9]:=

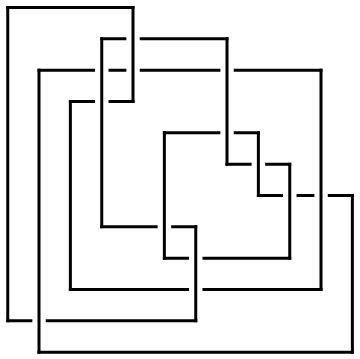
Reflect[ap_ArcPresentation] := ArcPresentation @@ ( (Last /@ Sort[Reverse /@ Position[ap, #]]) & /@ Range[Length[ap]] )

In[11]:=	Reflect[ap] // Draw
Out[11]=	-Graphics-

In[12]:=

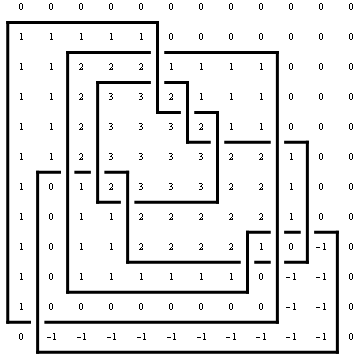
MinesweeperMatrix[ap_ArcPresentation] := Module[ {l, CurrentRow, c1, c2, k, s}, l = Length[ap]; CurrentRow = Table[0, {l}]; Table[ {c1, c2} = Sort[ap[[k]]]; s = Sign[{-1, 1}.ap[[k]]]; Do[ CurrentRow[[c]] += s, {c, c1, c2 - 1} ]; CurrentRow, {k, l} ] ];

In[14]:=	Draw[ap, OverlayMatrix -> MinesweeperMatrix[ap]]
Out[14]=	-Graphics-

In[15]:=	{Det[t^MinesweeperMatrix[ap]], Alexander[ap][t]} // Factor
Out[15]=	11 2 2 3 4 5 6 {(-1 + t) t (1 - 5 t + 13 t - 17 t + 13 t - 5 t + t ), 2 3 4 5 6 1 - 5 t + 13 t - 17 t + 13 t - 5 t + t -------------------------------------------} 3 t