Heegaard Floer Knot Homology: Difference between revisions
From Knot Atlas
Jump to navigationJump to search
DrorsRobot (talk | contribs) No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Manual TOC Sidebar}} |
{{Manual TOC Sidebar}} |
||
{{In Preparation}} |
|||
In 2007, [http://www.math.unizh.ch/user/jdroz/ Jean-Marie Droz] of the University of Zurich (working along with [http://www.math.unizh.ch/index.php?id=1819&no_cache=1&key1=578&no_cache=1 Anna Beliakova]) wrote a Python program to compute the (hat-version) Heegaard-Floer Knot Homology <math>\widehat{\operatorname{HFK}}(K)</math> of a knot <math>K</math>. His program is integrated into <code>KnotTheory`</code>, though to run it, you must have [http://python.org/ Python] as well as the Python library [http://psyco.sourceforge.net/ Psycho] installed on your system. |
In 2007, [http://www.math.unizh.ch/user/jdroz/ Jean-Marie Droz] of the University of Zurich (working along with [http://www.math.unizh.ch/index.php?id=1819&no_cache=1&key1=578&no_cache=1 Anna Beliakova]) wrote a Python program to compute the (hat-version) Heegaard-Floer Knot Homology <math>\widehat{\operatorname{HFK}}(K)</math> of a knot <math>K</math>. His program is integrated into <code>KnotTheory`</code>, though to run it, you must have [http://python.org/ Python] as well as the Python library [http://psyco.sourceforge.net/ Psycho] installed on your system. |
||
| Line 14: | Line 15: | ||
about= <nowiki>The Heegaard-Floer Knot Homology program was written by Jean-Marie Droz in 2007 at the University of Zurich, based on methods of Anna Beliakova's arXiv:07050669.</nowiki>}} |
about= <nowiki>The Heegaard-Floer Knot Homology program was written by Jean-Marie Droz in 2007 at the University of Zurich, based on methods of Anna Beliakova's arXiv:07050669.</nowiki>}} |
||
<!--END--> |
<!--END--> |
||
{| align=center |
|||
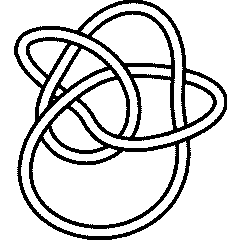
|[[Image:8_19.gif|thumb|180px|<center>[[8_19]]</center>]] |
|||
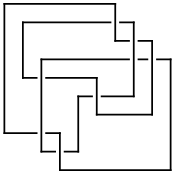
|[[Image:8_19_AP.gif|thumb|none|<center>in [[Arc Presentations|Arc Presentation]]</center>|180px]] |
|||
|} |
|||
The Heegaard-Floer Knot Homology is a categorification of the [[The Alexander-Conway Polynomial|Alexander polynomial]]. Let us test that for the knot [[8_19]]: |
The Heegaard-Floer Knot Homology is a categorification of the [[The Alexander-Conway Polynomial|Alexander polynomial]]. Let us test that for the knot [[8_19]]: |
||
Revision as of 11:30, 3 December 2007
In 2007, Jean-Marie Droz of the University of Zurich (working along with Anna Beliakova) wrote a Python program to compute the (hat-version) Heegaard-Floer Knot Homology of a knot . His program is integrated into KnotTheory`, though to run it, you must have Python as well as the Python library Psycho installed on your system.
(For In[1] see Setup)
|
| ||||||||
The Heegaard-Floer Knot Homology is a categorification of the Alexander polynomial. Let us test that for the knot 8_19:
In[3]:=
|
hfk = HFKHat[K = Knot[8, 19]][t, m]
|
Out[3]=
|
2 -3 m 5 2 6 3
m + t + -- + m t + m t
2
t
|
In[4]:=
|
{hfk /. m -> -1, Alexander[K][t]}
|
Out[4]=
|
-3 -2 2 3 -3 -2 2 3
{1 + t - t - t + t , 1 + t - t - t + t }
|
The knot 8_19 is the first knot in the Rolfsen Knot Table whose Heegaard-Floer Knot Homology is not "diagonal". Let us test that. The homology is "on diagonal", iff its Poincare polynomial, evaluated at , is a monomial:
In[5]:=
|
Select[AllKnots[{3, 8}], (Head[HFKHat[#][t, 1/t]] == Plus) &]
|
Out[5]=
|
{Knot[8, 19]}
|
In[6]:=
|
hfk /. m -> 1/t
|
Out[6]=
|
4 -2
-- + t
3
t
|