Brunnian link: Difference between revisions
(Starting article "Brunnian" link, partly from the Wikipedia article (which is partly written by me).) |
(explain) |
||
| Line 5: | Line 5: | ||
The name Brunnian is after Hermann Brunn, whose 1892 article ''Über Verkettung'' included examples of such links. |
The name Brunnian is after Hermann Brunn, whose 1892 article ''Über Verkettung'' included examples of such links. |
||
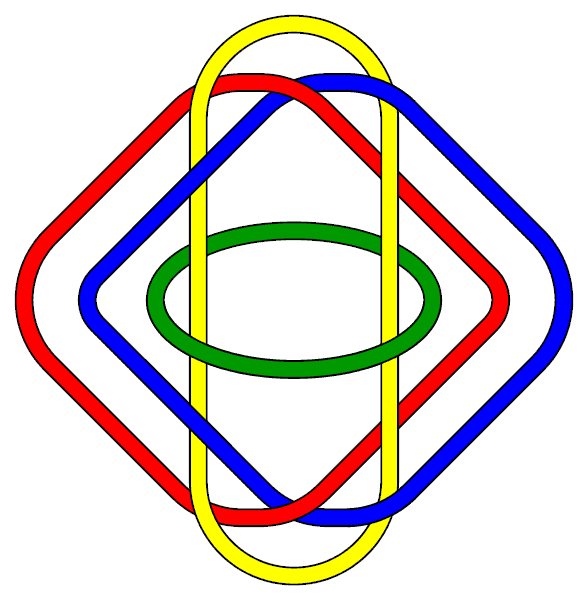
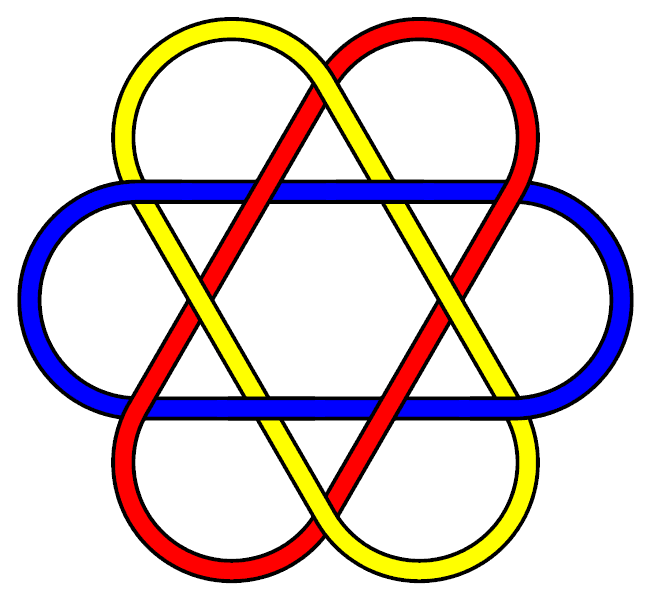
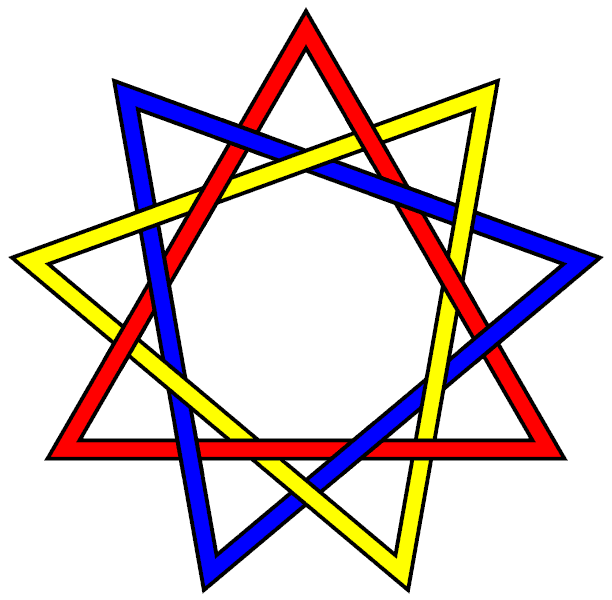
The best-known and simplest possible Brunnian link is the [[L6a4|Borromean rings]], a link of three unknots. However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: |
The best-known and simplest possible Brunnian link is the [[L6a4|Borromean rings]], a link of three unknots. (This is also the only Brunnian link contained in tables which don't include links with 12 or more crossings.) However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: |
||
<gallery> |
<gallery> |
||
Revision as of 18:10, 12 May 2006
A Brunnian link is a nontrivial link which becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops (so that there is no Hopf link between any two loops).
The name Brunnian is after Hermann Brunn, whose 1892 article Über Verkettung included examples of such links.
The best-known and simplest possible Brunnian link is the Borromean rings, a link of three unknots. (This is also the only Brunnian link contained in tables which don't include links with 12 or more crossings.) However for every number three or above, there are an infinite number of links with the Brunnian property containing that number of loops. Here are some relatively simple three-component Brunnian links which are not the same as the Borromean rings: