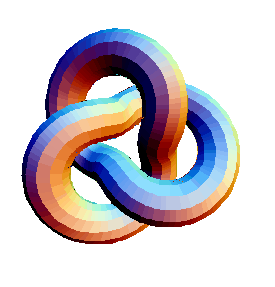Drawing with TubePlot

http://www.texteltdomdar.com

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

(For In[1] see Setup)

In[1]:= ?TubePlot TubePlot[gamma, {t, t0, t1}, r, opts] plots the space curve gamma with the variable t running from t0 to t1, as a tube of radius r. The available options are TubeSubdivision, TubeFraming and TubePlotPrelude. All other options are passed on to Graphics3D. TubePlot[TorusKnot[m, n], opts] produces a tube plot of the (m,n) torus knot.

Thus here's a thin unknot:

In[3]:=	Show[TubePlot[{Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.1]]
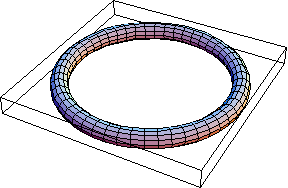
Out[3]=	-Graphics3D-

In[4]:= ?TubeSubdivision TubeSubdivision is an option for TubePlot. TubePlot[__, TubeSubdivision -> {l, m} draws the tube subdivided to l pieces lengthwise and m pieces around. The default is TubeSubdivision -> {50, 12}.

In[5]:= ?TubeFraming TubeFraming is an option for TubePlot. TubePlot[gamma, {t, __}, _, TubeFraming -> n] sets the framing of the tube (visible when TubeSubdivision -> {l, m} with small m) to be the vector n, which in itself may be a function of t. Thus TubeFraming -> {0,0,1} is "blackboard framing". TubeFraming -> Normal (default) uses the normal vector of the curve gamma.

In[6]:= ?TubePlotPrelude TubePlotPrelude is an option for TubePlot. Its value is passed to Graphics3D before the main part of the plot, allowing to set various graphics options. For example, TubePlotPrelude -> EdgeForm[{}] will suppress the drawing of edges between the polygons making up the tube. The default is TubePlotPrelude -> {}.

Here's the same unknot, made thicker and not as smooth:

In[8]:=	Show[TubePlot[ {Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.3, TubeSubdivision -> {6, 3} ]]
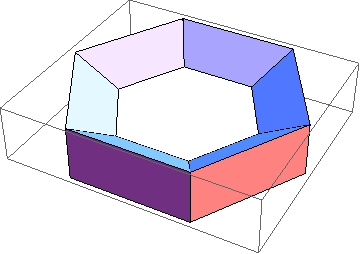
Out[8]=	-Graphics3D-

Let's play with the framing now:

In[10]:=	Show[TubePlot[ {Cos[t], Sin[t], 0}, {t, 0, 2Pi}, 0.2, TubeSubdivision -> {50, 2}, TubeFraming -> {Cos[2t]Cos[t], Cos[2t]Sin[t], Sin[3t]} ]]
Out[10]=	-Graphics3D-

Here's an example that uses a prelude and passes options on to Graphics3D:

In[12]:=	Show[TubePlot[ {Cos[2t], Sin[2t], 0} + 0.5{Cos[3t]Cos[2t], Cos[3t]Sin[2t], -Sin[3t]}, {t, 0, 2Pi}, 1/3, TubeSubdivision -> {280, 12}, TubeFraming -> {0,0,1}, TubePlotPrelude -> EdgeForm[{}], Boxed -> False, ViewPoint -> {0,0,1} ]]
Out[12]=	-Graphics3D-

The last example serves as the basis for the definition of TubePlot[TorusKnot[m, n]]. Here's a final example:

In[14]:=	Show[TubePlot[TorusKnot[3, 5]]]
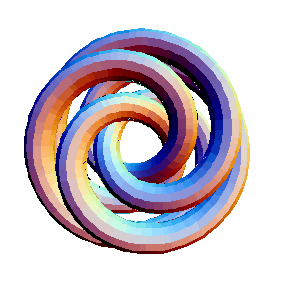
Out[14]=	-Graphics3D-

Standalone TubePlot

There may be some independent interest in the routine TubePlot, and hence it is available also as an independent package. Here it is: TubePlot.m (File:TubePlot.m).