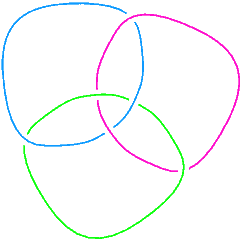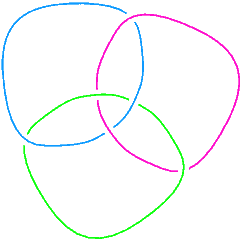Printable Manual

Return to the wiki manual.

Acknowledgement

This Atlas is partially (and indirectly) supported by NSERC grant RGPIN 262178. As a Wiki project, it doesn't make sense anymore to acknowledge individual contributors. Yet for historical purposes, here's our acknowledgement as of the conversion to Wiki formnat on August 2005:

• Jana Archibald, for writing the program Alexander[K, r].
• Sergei Chmutov, for spotting a typo.
• David De Wit, for a bug report.
• Ralph Furmaniak, for help with our link to Knotilus (see Gauss Codes).
• Stavros Garoufalidis, for jointly writing the program ColouredJones (see The Coloured Jones Polynomials).
• Thomas Gittings, for the minimum braid representatives for the knots with up to 10 crossings (see Braid Representatives).
• Jeremy Green, for his java implementation of Kh (see Khovanov Homology).
• Thang Le, for supplying some of the formulas used in the program ColouredJones (see The Coloured Jones Polynomials).
• Rick Litherland, for spotting a sneaky bug in the program KnotSignature.
• Charles Livingston, for allowing us to bundle data from his Table of Knot Invariants.
• Scott Morrison, for a bug report and for writing the programs to compute the HOMFLY-PT and Kauffman polynomials (see The HOMFLY-PT Polynomial and The Kauffman Polynomial).
• Bertrand Patureau-Mirand, for informing us of some mismatches in the link tables (now corrected).
• Jozef Przytycki, for correcting a typo.
• Stuart Rankin, for help with our link to Knotilus (see Gauss Codes).
• Emily Redelmeier, for writing the program DrawPD (see Drawing Planar Diagrams).
• Siddarth Sankaran, for writing the conversion program between Gauss codes and PD codes and for writing MorseLink and DrawMorseLink.
• Alexander Shumakovitch, for his help with signature computations (see The Determinant and the Signature).
• Alexander Stoimenow, for the knot presentations for the knots in the Rolfsen table and some further remarks.
• Z-X. Tao, for noticing problems with the knots 10_83 and 10_86.
• Morwen Thistlethwaite, for the pictures of links and of 11 crossing knots.
• Dylan Thurston, for writing an early routine to translate from Hoste-Thistlethwaite's DT codes to my "PD Presentations".

Setup

Start by downloading the file KnotTheory.zip (around 15MB), and unpack it. This will create a subdirectory KnotTheory/ in your current working directory. This done, no installation is required (though you may wish to check out Further Data Files and/or Setting the Path below). Start Mathematica and you're ready to go:

In[2]:= << KnotTheory`

Loading KnotTheory` version of March 22, 2011, 21:10:4.67737. Read more at http://katlas.org/wiki/KnotTheory.

Notice the little "prime" at the end of KnotTheory above. It is a backquote (find it on the upper left side of most keyboards) and not a quote, and it really has to be there for things to work.

Let us check that everything is working well:

In[3]:=	Alexander[Knot[6, 2]][t]
Out[3]=	-2 3 2 -3 - t + - + 3 t - t t

In[4]:= ?KnotTheoryVersion KnotTheoryVersion[] returns the date of the current version of the package KnotTheory`. KnotTheoryVersion[k] returns the kth field in KnotTheoryVersion[].

In[5]:= ?KnotTheoryVersionString KnotTheoryVersionString[] returns a string containing the date and time of the current version of the package KnotTheory`. It is generated from KnotTheoryVersion[].

In[6]:= ?KnotTheoryWelcomeMessage KnotTheoryWelcomeMessage[] returns a string containing the welcome message printed when KnotTheory` is first loaded.

Thus on the day this manual page was last changed, we had:

In[7]:=	{KnotTheoryVersion[], KnotTheoryVersionString[]}
Out[7]=	{{2011, 3, 22, 21, 10, 4.67737}, March 22, 2011, 21:10:4.67737}

In[8]:=	KnotTheoryWelcomeMessage[]
Out[8]=	Loading KnotTheory` version of March 22, 2011, 21:10:4.67737. Read more at http://katlas.org/wiki/KnotTheory.

In[9]:= ?KnotTheoryDirectory KnotTheoryDirectory[] returns the best guess KnotTheory` has for its location on the host computer. It can be reset by the user.

In[10]:=	KnotTheoryDirectory[]
Out[10]=	C:\Documents and Settings\pc\Documenti\Wolfram\KnotTheory

KnotTheoryDirectory may not work under some operating systems/environments. Please let Dror know if you encounter any difficulties.

Notes

Precomputed Data

KnotTheory` comes with a certain amount of precomputed data which is loaded "on demand" just when it is needed. When a precomputed data file is read by KnotTheory`, a notification message is displayed. To prevent these messages from appearing execute the command Off[KnotTheory::loading].

Further Data Files

To access the Hoste-Thistlethwaite enumeration of knots with 12 to 16 crossings (see Naming and Enumeration), also download either the file DTCodes4Knots12To16.tar.gz or the file DTCodes4Knots12To16.zip (about 9MB each), and unpack either one into the directory KnotTheory/.

Setting the Path

The directions above are written on the assumption that the package KnotTheory` (more precisely, the directory KnotTheory/ containing the files that make this package), is somewhere on your Mathematica search path. Usually this will be the case if KnotTheory/ is a subdirectory of your current working directory. If for some reason Mathematica cannot find KnotTheory`, you may tell it where to look in either of the following three ways. Assume KnotTheory/ is a subdirectory of FullPathToKnotTheory:

1. If you are using KnotTheory` rarely and you don't want to change system defaults, evaluate AppendTo[$Path,"FullPathToKnotTheory"] within Mathematica before attempting to load KnotTheory`.
2. If you plan to use KnotTheory` often, you may want to move the directory KnotTheory/ into one of the directories on your path. Evaluate $Path within Mathematica to see what those are.
3. Alternatively, you may permanently add FullPathToKnotTheory to your $Path. To do that, find your Mathematica base directory by evaluating $UserBaseDirectory (on Dror's laptop, this comes out to be C:\Users\Dror\AppData\Roaming\Mathematica), and then add the line AppendTo[$Path,"FullPathToKnotTheory/"] to the file $BaseDirectory/Kernel/init.m and restart Mathematica.

Naming and Enumeration

KnotTheory` comes loaded with some knot tables; currently, the Rolfsen table of prime knots with up to 10 crossings [Rolfsen], the Hoste-Thistlethwaite tables of prime knots with up to 16 crossings and the Thistlethwaite table of prime links with up to 11 crossings (see Knotscape):

(For In[1] see Setup)

In[2]:= ?Knot Knot[n, k] denotes the kth knot with n crossings in the Rolfsen table. Knot[n, Alternating, k] (for n between 11 and 16) denotes the kth alternating n-crossing knot in the Hoste-Thistlethwaite table. Knot[n, NonAlternating, k] denotes the kth non alternating n-crossing knot in the Hoste-Thistlethwaite table.

In[3]:= ?Link Link[n, Alternating, k] denotes the kth alternating n-crossing link in the Thistlethwaite table. Link[n, NonAlternating, k] denotes the kth non alternating n-crossing link in the Thistlethwaite table.

6_1

9_46

Thus, for example, let us verify that the knots 6_1 and 9_46 have the same Alexander polynomial:

In[4]:=	Alexander[Knot[6, 1]][t]
Out[4]=	2 5 - - - 2 t t

In[5]:=	Alexander[Knot[9, 46]][t]
Out[5]=	2 5 - - - 2 t t

L6a4

We can also check that the Borromean rings, L6a4 in the Thistlethwaite table, is a 3-component link:

In[6]:=	Length[Skeleton[Link[6, Alternating, 4]]]
Out[6]=	3

In[7]:= ?AllKnots AllKnots[] return a list of all knots with up to 11 crossings. AllKnots[n_] returns a list of all knots with n crossings, up to 16. AllKnots[{n_, m_}] returns a list of all knots with between n and m crossings, and AllKnots[n_, Alternating|NonAlternating] returns all knots with n crossings of the specified type.

In[8]:= ?AllLinks AllLinks[] return a list of all links with up to 11 crossings. AllLinks[n_] returns a list of all links with n crossings, up to 12.

Thus at the moment there are 1701936 knots and 5700 links known to KnotTheory`:

In[9]:=	Length /@ {AllKnots[{0,16}], AllLinks[{2,12}]}
Out[9]=	{1701936, 5700}

In[10]:=	Show[DrawPD[Knot[13, NonAlternating, 5016], {Gap -> 0.025}]]
Out[10]=	-Graphics-

(Shumakovitch had noticed that this nice knot has interesting Khovanov homology; see [Shumakovitch]).

T(5,3)

In addition to the tables, KnotTheory` also knows about torus knots:

In[11]:= ?TorusKnot TorusKnot[m, n] represents the (m,n) torus knot.

In[12]:= ?TorusKnots TorusKnots[n_] returns a list of all torus knots with up to n crossings.

For example, the torus knots T(5,3) and T(3,5) have different presentations with different numbers of crossings, but they are in fact isotopic, and hence they have the same invariants (and in particular the same type 3 Vassiliev invariant $V_{3}$):

In[13]:=	Crossings /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
Out[13]=	{10, 12}

In[14]:=	Vassiliev[3] /@ {TorusKnot[5, 3], TorusKnot[3, 5]}
Out[14]=	{20, 20}

KnotTheory` knows how to plot torus knots; see Drawing with TubePlot.

You can also use the function Knot to parse certain string representations of named knots:

In[15]:=	Knot /@ {"K11a14", "11a_14", "L8a1", "T(3,5)"}
Out[15]=	{Knot[11, Alternating, 14], If[11 a <= 10 && 14 <= NumberOfKnots[11 a, Alternating] + NumberOfKnots[11 a, NonAlternating], Knot @@ KnotTheory`Naming`s$3008], Link[8, Alternating, 1], TorusKnot[3, 5]}

In the opposite direction, the function NameString produces the standard name for a knot, used throughout the Knot Atlas.

In[16]:=	NameString /@ {Knot[11, Alternating, 14], TorusKnot[3,5]}
Out[16]=	{K11a14, T(3,5)}

References

[Rolfsen] ^  D. Rolfsen, Knots and Links, Publish or Perish, Mathematics Lecture Series 7, Wilmington 1976.

[Shumakovitch] ^  A. Shumakovitch, Torsion of the Khovanov Homology, arXiv:math.GT/0405474.

Presentations

KnotTheory` uses several presentations for knots/links.

• Planar Diagrams
  • Some further details
• Gauss Codes
• DT (Dowker-Thistlethwaite) Codes
• Braid Representatives
• MorseLink Presentations
• Arc Presentations
• Conway Notation

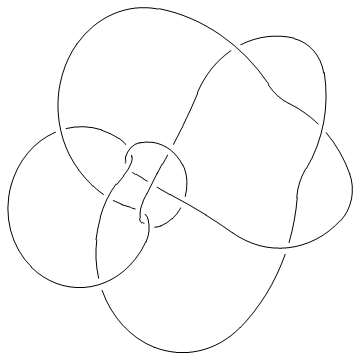
Planar Diagrams

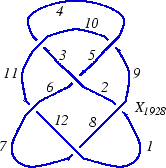
The PD notation

In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols $X_{ijkl}$ where $i$, $j$, $k$ and $l$ are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot above is:

$X_{1928}X_{3,10,4,11}X_{5362}X_{7,1,8,12}X_{9,4,10,5}X_{11,7,12,6}.$

(This of course is the Miller Institute knot, the mirror image of the knot 6_2)

(For In[1] see Setup)

In[2]:= ?PD PD[v1, v2, ...] represents a planar diagram whose vertices are v1, v2, .... PD also acts as a "type caster", so for example, PD[K] where K is a named knot (or link) returns the PD presentation of that knot.

In[3]:= PD::about The GaussCode to PD conversion was written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

In[4]:= ?X X[i,j,k,l] represents a crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counterclockwise through j, k and l. The (sometimes ambiguous) orientation of the upper strand is determined by the ordering of {j,l}.

Thus, for example, let us compute the determinant of the above knot:

In[5]:=

K = PD[ X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], X[7,1,8,12], X[9,4,10,5], X[11,7,12,6] ];

In[6]:=	Alexander[K][-1]
Out[6]=	-11

Some further details

In[7]:= ?Xp Xp[i,j,k,l] represents a positive (right handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from l to j regardless of the ordering of {j,l}. Presently Xp is only lightly supported.

In[8]:= ?Xm Xm[i,j,k,l] represents a negative (left handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from j to l regardless of the ordering of {j,l}. Presently Xm is only lightly supported.

In[9]:= ?P P[i,j] represents a bivalent vertex whose adjacent edges are i and j (i.e., a "Point" between the segment i and the segment j). Presently P is only lightly supported.

For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13:

In[10]:=

K1 = PD[ X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], X[7,1,8,13], X[9,4,10,5], X[11,7,12,6], P[12,13] ];

At the moment, many of our routines do not know to ignore such "extra points". But some do:

In[11]:=	Jones[K][q] == Jones[K1][q]
Out[11]=	True

In[12]:= ?Loop Loop[i] represents a crossingsless loop labeled i.

Hence we can verify that the A2 invariant of the unknot is $q^{-2}+1+q^{2}$:

In[13]:=	A2Invariant[Loop[1]][q]
Out[13]=	-2 2 1 + q + q

Gauss Codes

The Gauss Code of an $n$-crossing knot or link $L$ is obtained as follows:

• Number the crossings of $L$ from 1 to $n$ in an arbitrary manner.
• Order the components of $L$ is some arbitrary manner.
• Start "walking" along the first component of $L$, taking note of the numbers of the crossings you've gone through. If in a given crossing you cross on the "over" strand, write down the number of that crossing. If you cross on the "under" strand, write down the negative of the number of that crossing.
• Do the same for all other components of $L$ (if any).

The resulting list of signed integers (in the case of a knot) or list of lists of signed integers (in the case of a link) is called the Gauss Code of $L$. KnotTheory` has some rudimentary support for Gauss codes:

(For In[1] see Setup)

In[2]:= ?GaussCode GaussCode[i1, i2, ...] represents a knot via its Gauss Code following the conventions used by the knotilus website, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/html/start.html. Likewise GaussCode[l1, l2, ...] represents a link, where each of l1, l2,... is a list describing the code read along one component of the link. GaussCode also acts as a "type caster", so for example, GaussCode[K] where K is is a named knot (or link) returns the Gauss code of that knot.

Thus for example, the Gauss codes for the trefoil knot and the Borromean link are:

In[3]:=	GaussCode /@ {Knot[3, 1], Link[6, Alternating, 4]}
Out[3]=	{GaussCode[-1, 3, -2, 1, -3, 2], GaussCode[{1, -6, 5, -3}, {4, -1, 2, -5}, {6, -4, 3, -2}]}

3_1

L6a4

Ralph Furmaniak, working under the guidance of Stuart Rankin and Ortho Flint at the University of Western Ontario, wrote a web-based server called "Knotilus" that takes Gauss codes and outputs pictures of the desired knots and links in several standard image formats.

In[4]:= ?KnotilusURL KnotilusURL[K_] returns the URL of the knot/link K on the knotilus website, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/html/start.html.

Thus,

In[5]:=	KnotilusURL /@ {Knot[3, 1], Link[6, Alternating, 4]}
Out[5]=	{http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/-1,3,-2,1,-3,2/goTop.h\ tml, http://srankin.math.uwo.ca/cgi-bin/retrieve.cgi/1,-6,5,-3:4,-1,\ 2,-5:6,-4,3,-2/goTop.html}

• • DT (Dowker-Thistlethwaite) Codes
  • Braid Representatives
• Graphical Output
  • Drawing Planar Diagrams
    • How does it work?
  • Drawing Braids
• Structure and Operations
• Invariants
  • Invariants from Braid Theory
  • Three Dimensional Invariants
  • The Alexander-Conway Polynomial
  • The Determinant and the Signature
  • The Jones Polynomial
    • How is the Jones polynomial computed?
  • The Coloured Jones Polynomials
  • The A2 Invariant
  • The HOMFLY-PT Polynomial
  • The Kauffman Polynomial
  • Finite Type (Vassiliev) Invariants
  • Khovanov Homology
• Extras Included with KnotTheory`
  • Drawing with TubePlot
    • Standalone TubePlot
  • WikiLink - The Mediawiki Interface
  • Standalone WikiLink
• Lightly Documented Features
• Further Knot Theory Software
  • KnotPlot
  • Knotscape
• How to Edit this Manual...
• About this Manual...
• Bibliography