Planar Diagrams

KnotTheory`/Navigation  The Mathematica Package KnotTheory` Acknowledgement Setup Naming and Enumeration Presentations Planar Diagrams Some further details Gauss Codes DT (Dowker-Thistlethwaite) Codes Braid Representatives MorseLink Presentations Arc Presentations Conway Notation Graphical Input Graphical Output Drawing Planar Diagrams How does it work? Drawing MorseLink Presentations Drawing Braids Structure and Operations Invariants Invariants from Braid Theory Three Dimensional Invariants The Alexander-Conway Polynomial The Multivariable Alexander Polynomial The Determinant and the Signature The Jones Polynomial How is the Jones polynomial computed? The Coloured Jones Polynomials The A2 Invariant Quantum knot invariants The HOMFLY-PT Polynomial The Kauffman Polynomial Finite Type (Vassiliev) Invariants Khovanov Homology Heegaard Floer Knot Homology R-Matrix Invariants Extras Included with KnotTheory` Drawing with TubePlot Standalone_TubePlot Using the LinKnot package WikiLink QuantumGroups` Lightly Documented Features A Sample KnotTheory` Session Further Usage Example Prime Links with a Non-Prime Component "Rubberband" Brunnian Links Identifying Knots within a List Cabling Burau's Theorem Further Knot Theory Software KnotPlot Knotscape Xknots Extending/Modifying KnotTheory` Bugs How to Edit this Manual...

The PD notation

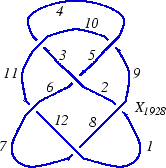
In the "Planar Diagrams" (PD) presentation we present every knot or link diagram by labeling its edges (with natural numbers, 1,...,n, and with increasing labels as we go around each component) and by a list crossings presented as symbols $X_{ijkl}$ where $i$, $j$, $k$ and $l$ are the labels of the edges around that crossing, starting from the incoming lower edge and proceeding counterclockwise. Thus for example, the PD presentation of the knot above is:

$X_{1928}X_{3,10,4,11}X_{5362}X_{7,1,8,12}X_{9,4,10,5}X_{11,7,12,6}.$

(This of course is the Miller Institute knot, the mirror image of the knot 6_2)

(For In[1] see Setup)

In[1]:= ?PD PD[v1, v2, ...] represents a planar diagram whose vertices are v1, v2, .... PD also acts as a "type caster", so for example, PD[K] where K is is a named knot (or link) returns the PD presentation of that knot.

In[2]:= PD::about The PD to GaussCode and to MorseLink conversions were written by Siddarth Sankaran at the University of Toronto in the summer of 2005.

In[3]:= ?X X[i,j,k,l] represents a crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counterclockwise through j, k and l. The (sometimes ambiguous) orientation of the upper strand is determined by the ordering of {j,l}.

Thus, for example, let us compute the determinant of the above knot:

In[4]:=

K = PD[X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], X[7,1,8,12], X[9,4,10,5], X[11,7,12,6]];

In[5]:=	Alexander[K][-1]
Out[5]=	-11

Some further details

In[6]:= ?Xp Xp[i,j,k,l] represents a positive (right handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from l to j regardless of the ordering of {j,l}. Presently Xp is only lightly supported.

In[7]:= ?Xm Xm[i,j,k,l] represents a negative (left handed) crossing between the edges labeled i, j, k and l starting from the incoming lower strand i and going counter clockwise through j, k and l. The upper strand is therefore oriented from j to l regardless of the ordering of {j,l}. Presently Xm is only lightly supported.

In[8]:= ?P P[i,j] represents a bivalent vertex whose adjacent edges are i and j (i.e., a "Point" between the segment i and the segment j). Presently P is only lightly supported.

For example, we could add an extra "point" on the Miller Institute knot, splitting edge 12 into two pieces, labeled 12 and 13:

In[9]:=

K1 = PD[X[1,9,2,8], X[3,10,4,11], X[5,3,6,2], X[7,1,8,13], X[9,4,10,5], X[11,7,12,6], P[12,13]];

At the moment, many of our routines do not know to ignore such "extra points". But some do:

In[10]:=	Jones[K][q] == Jones[K1][q]
Out[10]=	True

In[11]:= ?Loop Loop[i] represents a crossingsless loop labeled i.

Hence we can verify that the A2 invariant of the unknot is $q^{-2}+1+q^{2}$:

In[12]:=	A2Invariant[Loop[1]][q]
Out[12]=	-2 2 1 + q + q