MorseLink Presentations: Difference between revisions
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
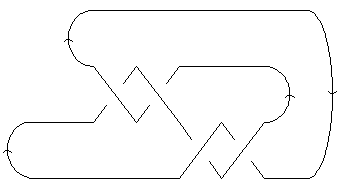
[[Image:MLPres0.png|frame|center|A diagram of the knot [[4_1]] ]] |
[[Image:MLPres0.png|frame|center|A diagram of the knot [[4_1]] ]] |
||
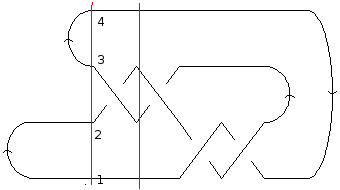
We'll fix the chosen axis to be horizontal and to the right, and we'll number the strands at each interval from bottom to top. |
We'll fix the chosen axis to be horizontal and to the right, and we'll number the strands at each interval from bottom to top. Clearly the first event to take place is a cup, creating strands 1 and 2, and directed from 1 to 2. The next event is also a cup; this time, the strands 3 and 4 are created, from 3 to 4. So the first two elements of our MorseLink presentation are <code>{Cup[1,2], Cup[3,4], ...}</code>. |
||
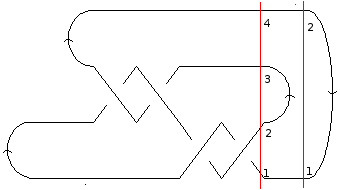
[[Image:MLPres1.png|50px|frame|left|A crossing event]]The next event to take place is a crossing. This crossing has strand 2 going under strand 3; following the orientations, strand 2 moves to the right through the crossing, while strand 3 comes from the left. Since the chosen axis is pointing to the right, this event is described as <code>X[2, Under, Up, Down]</code>. We may proceed in a similar way for the rest of the crossings. |
|||
<br style="clear:both" /> |
|||
[[Image:MLPres2.png|frame|left|Two cap events]]After three more crossings, we encounter two cap events. The first annihilates strands 2 and 3, and is directed from 2 to 3. The second annihilates strands 1 and 2, but is directed from 2 to 1. So our MorseLink presentation for the knot [[4_1]] is given by: <code>MorseLink[Cup[1,2], Cup[3,4], X[2 , Under, Up, Down], X[2, Under, Down, Up], X[1, Over, Down, Up], X[1, Over, Up, Down], Cap[2,3], Cap[2,1]]</code>. |
|||
<br style="clear:both" /> |
|||
Revision as of 13:25, 2 September 2005
This page is under construction...
The MorseLink presentation describes an oriented knot or a link diagram as a sequence of 'events'. To begin, we fix an axis in the plane, so that each event in the MorseLink description occurs in successive intervals along this axis. The 'events' that comprise a knot or link are 'cups' (creations), 'caps' (annihilations), and crossings, where cups and caps are the minima and maxima (resp.) relative to the chosen axis. The conventions used by MorseLink are as follows:
- Cup[m,n] is a creation, where the new strands are in position m and n, with m and n differing by 1, and is directed from m to n.
- Cap[m,n] is an annihilation of the strands m and n, again with m and n differing by 1, and is directed from m to n.
- X[n, d, a, b] is a crossing of the n-th and the (n+1)-th strands. 'd' signifies whether the n-th strand goes 'Over' or 'Under' the (n+1)-th strand. 'a' indicates whether the n-th strand is moving 'Up' or 'Down' through the crossing, relative to the chosen axis; 'b' does the same for the (n+1)-th strand.
For concreteness, let us find a MorseLink presentation of the knot 4_1, based on the following diagram:
We'll fix the chosen axis to be horizontal and to the right, and we'll number the strands at each interval from bottom to top. Clearly the first event to take place is a cup, creating strands 1 and 2, and directed from 1 to 2. The next event is also a cup; this time, the strands 3 and 4 are created, from 3 to 4. So the first two elements of our MorseLink presentation are {Cup[1,2], Cup[3,4], ...}.
The next event to take place is a crossing. This crossing has strand 2 going under strand 3; following the orientations, strand 2 moves to the right through the crossing, while strand 3 comes from the left. Since the chosen axis is pointing to the right, this event is described as X[2, Under, Up, Down]. We may proceed in a similar way for the rest of the crossings.
After three more crossings, we encounter two cap events. The first annihilates strands 2 and 3, and is directed from 2 to 3. The second annihilates strands 1 and 2, but is directed from 2 to 1. So our MorseLink presentation for the knot 4_1 is given by: MorseLink[Cup[1,2], Cup[3,4], X[2 , Under, Up, Down], X[2, Under, Down, Up], X[1, Over, Down, Up], X[1, Over, Up, Down], Cap[2,3], Cap[2,1]].