10 165

10_164

K11a1

Visit 10 165's page at the Knot Server (KnotPlot driven, includes 3D interactive images!) Visit [${\textrm {KnotilusURL}}({\textrm {GaussCode}}())$ 10 165's page] at Knotilus! Visit 10 165's page at the original Knot Atlas! 10 165 Quick Notes

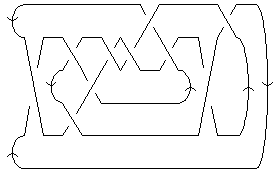
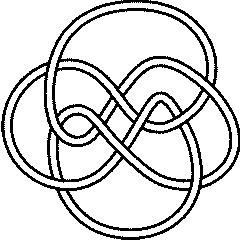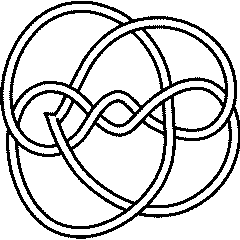Warning. In 1973 K. Perko noticed that the knots that were later labeled 10₁₆₁ and 10₁₆₂ in Rolfsen's tables (which were published in 1976 and were based on earlier tables by Little (1900) and Conway (1970)) are in fact the same. In our table we removed Rolfsen's 10₁₆₂ and renumbered the subsequent knots, so that our 10 crossings total is 165, one less than Rolfsen's 166. Read more: [1] [2] [3] [4] [5].

Knot presentations

Planar diagram presentation	X1627 X7,18,8,19 X3948 X17,3,18,2 X5,15,6,14 X9,17,10,16 X15,11,16,10 X11,5,12,4 X20,14,1,13 X12,20,13,19
Gauss code	-1, 4, -3, 8, -5, 1, -2, 3, -6, 7, -8, -10, 9, 5, -7, 6, -4, 2, 10, -9
Dowker-Thistlethwaite code	6 8 14 18 16 4 -20 10 2 -12
Conway Notation	[8*2:.-20]

Minimum Braid Representative: Length is 0, width is 1. Braid index is 1.

A Morse Link Presentation:

Three dimensional invariants

Symmetry type Reversible Unknotting number 2 3-genus 2 Bridge index 3 Super bridge index Missing Nakanishi index 1 Maximal Thurston-Bennequin number [1][-11] Hyperbolic Volume 11.6031 A-Polynomial See Data:10 165/A-polynomial

[edit Notes for 10 165's three dimensional invariants]

Four dimensional invariants

Smooth 4 genus $1$ Topological 4 genus $1$ Concordance genus $2$ Rasmussen s-Invariant 2

[edit Notes for 10 165's four dimensional invariants]

Polynomial invariants

Alexander polynomial	$-2t^{2}+10t-15+10t^{-1}-2t^{-2}$
Conway polynomial	$-2z^{4}+2z^{2}+1$
2nd Alexander ideal (db, data sources)	$\{1\}$
Determinant and Signature	{ 39, 2 }
Jones polynomial	$q^{9}-3q^{8}+4q^{7}-6q^{6}+7q^{5}-6q^{4}+6q^{3}-4q^{2}+2q$
HOMFLY-PT polynomial (db, data sources)	$-z^{4}a^{-4}-z^{4}a^{-6}+2z^{2}a^{-2}-z^{2}a^{-6}+z^{2}a^{-8}+a^{-2}+a^{-4}-a^{-6}$
Kauffman polynomial (db, data sources)	$2z^{8}a^{-6}+2z^{8}a^{-8}+4z^{7}a^{-5}+7z^{7}a^{-7}+3z^{7}a^{-9}+3z^{6}a^{-4}-2z^{6}a^{-6}-4z^{6}a^{-8}+z^{6}a^{-10}+z^{5}a^{-3}-10z^{5}a^{-5}-22z^{5}a^{-7}-11z^{5}a^{-9}-3z^{4}a^{-4}-2z^{4}a^{-6}-2z^{4}a^{-8}-3z^{4}a^{-10}+3z^{3}a^{-3}+11z^{3}a^{-5}+18z^{3}a^{-7}+10z^{3}a^{-9}+3z^{2}a^{-2}+z^{2}a^{-4}-2z^{2}a^{-6}+2z^{2}a^{-8}+2z^{2}a^{-10}-za^{-3}-5za^{-5}-5za^{-7}-za^{-9}-a^{-2}+a^{-4}+a^{-6}$
The A2 invariant	$2q^{-2}-q^{-4}+2q^{-8}+2q^{-12}-2q^{-20}+q^{-22}-q^{-24}-q^{-26}+q^{-28}$
The G2 invariant	$q^{-8}+2q^{-10}-q^{-12}+2q^{-14}-2q^{-16}+q^{-18}-2q^{-20}+4q^{-24}-4q^{-26}+9q^{-28}-12q^{-30}+13q^{-32}-6q^{-34}-7q^{-36}+24q^{-38}-33q^{-40}+29q^{-42}-15q^{-44}-7q^{-46}+33q^{-48}-39q^{-50}+36q^{-52}-12q^{-54}-17q^{-56}+36q^{-58}-34q^{-60}+13q^{-62}+15q^{-64}-35q^{-66}+40q^{-68}-22q^{-70}-q^{-72}+23q^{-74}-45q^{-76}+47q^{-78}-37q^{-80}+11q^{-82}+11q^{-84}-35q^{-86}+48q^{-88}-38q^{-90}+21q^{-92}-3q^{-94}-25q^{-96}+38q^{-98}-31q^{-100}+6q^{-102}+19q^{-104}-35q^{-106}+36q^{-108}-11q^{-110}-18q^{-112}+38q^{-114}-42q^{-116}+32q^{-118}-10q^{-120}-17q^{-122}+31q^{-124}-29q^{-126}+22q^{-128}-7q^{-130}-5q^{-132}+8q^{-134}-9q^{-136}+5q^{-138}-2q^{-140}+q^{-142}$

Further Quantum Invariants

Further quantum knot invariants for 10_165.

A1 Invariants.

Weight	Invariant
1	$2q^{-1}-2q^{-3}+2q^{-5}+q^{-9}+q^{-11}-2q^{-13}+q^{-15}-2q^{-17}+q^{-19}$
2	$1+q^{-2}-3q^{-4}+4q^{-6}+4q^{-8}-9q^{-10}+3q^{-12}+8q^{-14}-8q^{-16}-2q^{-18}+8q^{-20}+q^{-22}-6q^{-24}+3q^{-26}+5q^{-28}-7q^{-30}-4q^{-32}+7q^{-34}-3q^{-36}-8q^{-38}+8q^{-40}+4q^{-42}-8q^{-44}+2q^{-46}+6q^{-48}-3q^{-50}-2q^{-52}+q^{-54}$
3	$2q-2q^{-1}+3q^{-5}+7q^{-7}-7q^{-9}-18q^{-11}+9q^{-13}+31q^{-15}+2q^{-17}-42q^{-19}-17q^{-21}+45q^{-23}+33q^{-25}-31q^{-27}-42q^{-29}+13q^{-31}+40q^{-33}+7q^{-35}-32q^{-37}-22q^{-39}+20q^{-41}+30q^{-43}-8q^{-45}-36q^{-47}+q^{-49}+37q^{-51}+4q^{-53}-42q^{-55}-10q^{-57}+38q^{-59}+20q^{-61}-38q^{-63}-29q^{-65}+29q^{-67}+40q^{-69}-11q^{-71}-42q^{-73}-5q^{-75}+37q^{-77}+23q^{-79}-23q^{-81}-31q^{-83}+4q^{-85}+26q^{-87}+8q^{-89}-15q^{-91}-14q^{-93}+5q^{-95}+9q^{-97}+2q^{-99}-3q^{-101}-2q^{-103}+q^{-105}$

A2 Invariants.

Weight	Invariant
1,0	$2q^{-2}-q^{-4}+2q^{-8}+2q^{-12}-2q^{-20}+q^{-22}-q^{-24}-q^{-26}+q^{-28}$
1,1	$2q^{-2}-2q^{-8}+6q^{-10}+4q^{-12}+8q^{-16}-28q^{-18}+56q^{-20}-82q^{-22}+106q^{-24}-126q^{-26}+128q^{-28}-102q^{-30}+56q^{-32}+2q^{-34}-67q^{-36}+126q^{-38}-172q^{-40}+204q^{-42}-217q^{-44}+204q^{-46}-172q^{-48}+122q^{-50}-72q^{-52}+4q^{-54}+58q^{-56}-98q^{-58}+119q^{-60}-118q^{-62}+108q^{-64}-78q^{-66}+50q^{-68}-30q^{-70}+12q^{-72}-4q^{-74}+q^{-76}$
2,0	$q^{-2}+2q^{-4}-3q^{-6}-q^{-8}+7q^{-10}+5q^{-12}-4q^{-14}-4q^{-16}+3q^{-18}+4q^{-20}-5q^{-22}-2q^{-24}+4q^{-26}+2q^{-28}+2q^{-30}+q^{-32}+q^{-34}+q^{-38}-q^{-40}-6q^{-42}-4q^{-44}+q^{-46}+q^{-48}-6q^{-50}-q^{-52}+5q^{-54}+4q^{-56}-2q^{-58}-3q^{-60}+5q^{-62}+3q^{-64}-q^{-66}-3q^{-68}-q^{-70}+q^{-72}$

A3 Invariants.

Weight	Invariant
0,1,0	$3q^{-4}-q^{-6}-3q^{-8}+5q^{-10}+q^{-12}-4q^{-14}+8q^{-16}+3q^{-18}-3q^{-20}+6q^{-22}-4q^{-26}-q^{-28}-2q^{-30}-5q^{-34}+4q^{-38}-4q^{-40}-q^{-42}+6q^{-44}-3q^{-46}+5q^{-50}-5q^{-52}+q^{-54}+q^{-56}-2q^{-58}+q^{-60}$
1,0,0	$2q^{-3}-q^{-5}+q^{-7}+2q^{-11}+2q^{-15}+q^{-17}-q^{-23}-2q^{-27}+q^{-29}-q^{-31}-q^{-35}+q^{-37}$

A4 Invariants.

Weight	Invariant
0,1,0,0	$3q^{-6}-2q^{-10}+q^{-12}+4q^{-14}+q^{-16}-4q^{-18}+3q^{-20}+9q^{-22}+q^{-24}-2q^{-26}+9q^{-28}+8q^{-30}-4q^{-32}-q^{-34}+2q^{-36}-5q^{-38}-12q^{-40}-3q^{-42}-2q^{-44}-10q^{-46}+10q^{-50}-3q^{-54}+9q^{-56}+6q^{-58}-5q^{-60}-4q^{-62}+4q^{-64}-5q^{-68}+3q^{-72}-q^{-74}-q^{-76}+q^{-78}$
1,0,0,0	$2q^{-4}-q^{-6}+q^{-8}+q^{-10}+2q^{-14}+2q^{-18}+q^{-20}+q^{-22}-q^{-28}-q^{-30}-2q^{-34}+q^{-36}-q^{-38}-q^{-44}+q^{-46}$

B2 Invariants.

Weight	Invariant
0,1	$3q^{-4}-3q^{-6}+5q^{-8}-7q^{-10}+9q^{-12}-8q^{-14}+8q^{-16}-5q^{-18}+3q^{-20}+2q^{-22}-6q^{-24}+10q^{-26}-13q^{-28}+16q^{-30}-16q^{-32}+15q^{-34}-12q^{-36}+8q^{-38}-4q^{-40}-q^{-42}+4q^{-44}-7q^{-46}+8q^{-48}-9q^{-50}+7q^{-52}-7q^{-54}+5q^{-56}-2q^{-58}+q^{-60}$
1,0	$3q^{-6}+q^{-8}-2q^{-10}-4q^{-12}-q^{-14}+6q^{-16}+5q^{-18}-3q^{-20}-6q^{-22}+q^{-24}+10q^{-26}+4q^{-28}-6q^{-30}-5q^{-32}+6q^{-34}+7q^{-36}-3q^{-38}-8q^{-40}+7q^{-44}+q^{-46}-7q^{-48}-3q^{-50}+4q^{-52}+3q^{-54}-5q^{-56}-5q^{-58}+3q^{-60}+6q^{-62}-2q^{-64}-9q^{-66}-2q^{-68}+8q^{-70}+7q^{-72}-5q^{-74}-8q^{-76}+3q^{-78}+9q^{-80}+q^{-82}-6q^{-84}-4q^{-86}+4q^{-88}+3q^{-90}-2q^{-92}-2q^{-94}+q^{-98}$

D4 Invariants.

Weight	Invariant
1,0,0,0	$3q^{-6}-2q^{-8}+2q^{-10}-3q^{-12}+7q^{-14}-5q^{-16}+6q^{-18}-6q^{-20}+9q^{-22}-3q^{-24}+7q^{-26}+2q^{-30}+4q^{-32}-4q^{-34}+6q^{-36}-12q^{-38}+8q^{-40}-15q^{-42}+10q^{-44}-14q^{-46}+10q^{-48}-10q^{-50}+8q^{-52}-5q^{-54}+4q^{-56}+q^{-58}-q^{-60}+3q^{-62}-5q^{-64}+8q^{-66}-7q^{-68}+6q^{-70}-7q^{-72}+6q^{-74}-5q^{-76}+3q^{-78}-2q^{-80}+q^{-82}$

G2 Invariants.

Weight

Invariant

1,0

$q^{-8}+2q^{-10}-q^{-12}+2q^{-14}-2q^{-16}+q^{-18}-2q^{-20}+4q^{-24}-4q^{-26}+9q^{-28}-12q^{-30}+13q^{-32}-6q^{-34}-7q^{-36}+24q^{-38}-33q^{-40}+29q^{-42}-15q^{-44}-7q^{-46}+33q^{-48}-39q^{-50}+36q^{-52}-12q^{-54}-17q^{-56}+36q^{-58}-34q^{-60}+13q^{-62}+15q^{-64}-35q^{-66}+40q^{-68}-22q^{-70}-q^{-72}+23q^{-74}-45q^{-76}+47q^{-78}-37q^{-80}+11q^{-82}+11q^{-84}-35q^{-86}+48q^{-88}-38q^{-90}+21q^{-92}-3q^{-94}-25q^{-96}+38q^{-98}-31q^{-100}+6q^{-102}+19q^{-104}-35q^{-106}+36q^{-108}-11q^{-110}-18q^{-112}+38q^{-114}-42q^{-116}+32q^{-118}-10q^{-120}-17q^{-122}+31q^{-124}-29q^{-126}+22q^{-128}-7q^{-130}-5q^{-132}+8q^{-134}-9q^{-136}+5q^{-138}-2q^{-140}+q^{-142}$

.

Computer Talk

The above data is available with the Mathematica package KnotTheory`, as shown in the (simulated) Mathematica session below. Your input (in red) is realistic; all else should have the same content as in a real mathematica session, but with different formatting. This Mathematica session is also available (albeit only for the knot 5_2) as the notebook PolynomialInvariantsSession.nb.

(The path below may be different on your system, and possibly also the KnotTheory` date)

In[1]:=

AppendTo[$Path, "C:/drorbn/projects/KAtlas/"]; << KnotTheory`

Loading KnotTheory` version of August 31, 2006, 11:25:27.5625. Read more at http://katlas.math.toronto.edu/wiki/KnotTheory.

In[3]:=

K = Knot["10 165"];

In[4]:=

Alexander[K][t]

KnotTheory::loading: Loading precomputed data in PD4Knots`.

Out[4]=

$-2t^{2}+10t-15+10t^{-1}-2t^{-2}$

In[5]:=

Conway[K][z]

Out[5]=

$-2z^{4}+2z^{2}+1$

In[6]:=

Alexander[K, 2][t]

KnotTheory::credits: The program Alexander[K, r] to compute Alexander ideals was written by Jana Archibald at the University of Toronto in the summer of 2005.

Out[6]=

$\{1\}$

In[7]:=

{KnotDet[K], KnotSignature[K]}

Out[7]=

{ 39, 2 }

In[8]:=

Jones[K][q]

KnotTheory::loading: Loading precomputed data in Jones4Knots`.

Out[8]=

$q^{9}-3q^{8}+4q^{7}-6q^{6}+7q^{5}-6q^{4}+6q^{3}-4q^{2}+2q$

In[9]:=

HOMFLYPT[K][a, z]

KnotTheory::credits: The HOMFLYPT program was written by Scott Morrison.

Out[9]=

$-z^{4}a^{-4}-z^{4}a^{-6}+2z^{2}a^{-2}-z^{2}a^{-6}+z^{2}a^{-8}+a^{-2}+a^{-4}-a^{-6}$

In[10]:=

Kauffman[K][a, z]

KnotTheory::loading: Loading precomputed data in Kauffman4Knots`.

Out[10]=

$2z^{8}a^{-6}+2z^{8}a^{-8}+4z^{7}a^{-5}+7z^{7}a^{-7}+3z^{7}a^{-9}+3z^{6}a^{-4}-2z^{6}a^{-6}-4z^{6}a^{-8}+z^{6}a^{-10}+z^{5}a^{-3}-10z^{5}a^{-5}-22z^{5}a^{-7}-11z^{5}a^{-9}-3z^{4}a^{-4}-2z^{4}a^{-6}-2z^{4}a^{-8}-3z^{4}a^{-10}+3z^{3}a^{-3}+11z^{3}a^{-5}+18z^{3}a^{-7}+10z^{3}a^{-9}+3z^{2}a^{-2}+z^{2}a^{-4}-2z^{2}a^{-6}+2z^{2}a^{-8}+2z^{2}a^{-10}-za^{-3}-5za^{-5}-5za^{-7}-za^{-9}-a^{-2}+a^{-4}+a^{-6}$

"Similar" Knots (within the Atlas)

Same Alexander/Conway Polynomial: {K11n34, K11n42, ...}

Same Jones Polynomial (up to mirroring, $q\leftrightarrow q^{-1}$): {...}

Vassiliev invariants

V2 and V3:

(2, 3)

V2,1 through V6,9:

V2,1 V3,1 V4,1 V4,2 V4,3 V5,1 V5,2 V5,3 V5,4 V6,1 V6,2 V6,3 V6,4 V6,5 V6,6 V6,7 V6,8 V6,9 $8$ $24$ $32$ ${\frac {316}{3}}$ ${\frac {92}{3}}$ $192$ $464$ $128$ $88$ ${\frac {256}{3}}$ $288$ ${\frac {2528}{3}}$ ${\frac {736}{3}}$ ${\frac {29311}{15}}$ ${\frac {1276}{15}}$ ${\frac {47524}{45}}$ $-{\frac {415}{9}}$ ${\frac {2191}{15}}$

V_2,1 through V_6,9 were provided by Petr Dunin-Barkowski <barkovs@itep.ru>, Andrey Smirnov <asmirnov@itep.ru>, and Alexei Sleptsov <sleptsov@itep.ru> and uploaded on October 2010 by User:Drorbn. Note that they are normalized differently than V₂ and V₃.

Khovanov Homology

The coefficients of the monomials $t^{r}q^{j}$ are shown, along with their alternating sums $\chi$ (fixed $j$, alternation over $r$). The squares with yellow highlighting are those on the "critical diagonals", where $j-2r=s+1$ or $j-2r=s-1$, where $s=$2 is the signature of 10 165. Nonzero entries off the critical diagonals (if any exist) are highlighted in red.

\   r    \    j   \ 0 1 2 3 4 5 6 7 8 χ 19                 1 1 17               2   -2 15             2 1   1 13           4 2     -2 11         3 2       1 9       3 4         1 7     3 3           0 5   1 3             2 3 1 3               -2 1 2                 2

Integral Khovanov Homology (db, data source)

$\dim {\mathcal {G}}_{2r+i}\operatorname {KH} _{\mathbb {Z} }^{r}$ $i=1$ $i=3$ $r=0$ ${\mathbb {Z} }^{2}$ ${\mathbb {Z} }$ $r=1$ ${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}$ ${\mathbb {Z} }$ $r=2$ ${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=3$ ${\mathbb {Z} }^{3}\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=4$ ${\mathbb {Z} }^{4}\oplus {\mathbb {Z} }_{2}^{3}$ ${\mathbb {Z} }^{3}$ $r=5$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}^{4}$ ${\mathbb {Z} }^{4}$ $r=6$ ${\mathbb {Z} }^{2}\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=7$ ${\mathbb {Z} }\oplus {\mathbb {Z} }_{2}^{2}$ ${\mathbb {Z} }^{2}$ $r=8$ ${\mathbb {Z} }_{2}$ ${\mathbb {Z} }$

The Coloured Jones Polynomials

The Coloured Jones Polynomials (in the $n+1$-dimensional representation of $sl(2)$)

$n$	$J_{n}$
2	Not Available
3	Not Available
4	Not Available
5	Not Available
6	Not Available
7	Not Available

Computer Talk

Much of the above data can be recomputed by Mathematica using the package KnotTheory`. See A Sample KnotTheory` Session.

In[1]:=	<< KnotTheory`
Loading KnotTheory` (version of August 29, 2005, 15:27:48)...
In[2]:=	PD[Knot[0, 1]]
Out[2]=	PD[Loop[1]]
In[3]:=	GaussCode[Knot[0, 1]]
Out[3]=	GaussCode[]
In[4]:=	DTCode[Knot[0, 1]]
Out[4]=	DTCode[]
In[5]:=	br = BR[Knot[0, 1]]
Out[5]=	BR[1, {}]
In[6]:=	{First[br], Crossings[br]}
Out[6]=	{1, 0}
In[7]:=	BraidIndex[Knot[0, 1]]
Out[7]=	1
In[8]:=	Show[DrawMorseLink[Knot[0, 1]]]
Out[8]=	-Graphics-
In[9]:=	(#[Knot[0, 1]]&) /@ {SymmetryType, UnknottingNumber, ThreeGenus, BridgeIndex, SuperBridgeIndex, NakanishiIndex}
Out[9]=	{, 0, 0, 1, NotAvailable, NotAvailable}
In[10]:=	alex = Alexander[Knot[0, 1]][t]
Out[10]=	1
In[11]:=	Conway[Knot[0, 1]][z]
Out[11]=	1
In[12]:=	Select[AllKnots[], (alex === Alexander[#][t])&]
Out[12]=	{Knot[0, 1], Knot[11, NonAlternating, 34], Knot[11, NonAlternating, 42]}
In[13]:=	{KnotDet[Knot[0, 1]], KnotSignature[Knot[0, 1]]}
Out[13]=	{1, 0}
In[14]:=	Jones[Knot[0, 1]][q]
Out[14]=	1
In[15]:=	Select[AllKnots[], (J === Jones[#][q] || (J /. q-> 1/q) === Jones[#][q])&]
Out[15]=	{Knot[0, 1]}
In[16]:=	A2Invariant[Knot[0, 1]][q]
Out[16]=	-2 2 1 + q + q
In[17]:=	HOMFLYPT[Knot[0, 1]][a, z]
Out[17]=	1
In[18]:=	Kauffman[Knot[0, 1]][a, z]
Out[18]=	1
In[19]:=	{Vassiliev[2][Knot[0, 1]], Vassiliev[3][Knot[0, 1]]}
Out[19]=	{0, 0}
In[20]:=	Kh[Knot[0, 1]][q, t]
Out[20]=	1 - + q q

See/edit the Rolfsen_Splice_Template. Back to the top.

10_164 K11a1