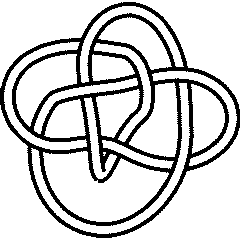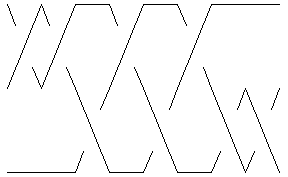The first step is to load KnotTheory` as in the Setup section:
In[1]:= << KnotTheory`
Loading KnotTheory` (version of September 14, 2005, 13:37:36)...
Let us now introduce the four star knots that will accompany us throughout this session:
In[2]:=
|
K = Knot[8, 17];
K11 = Knot[11, Alternating, 231];
L = Link[8, NonAlternating, 6];
TK = TorusKnot[7,5];
|
In[3]:=
|
PD[K]
|
Out[3]=
|
PD[X[6, 2, 7, 1], X[14, 8, 15, 7], X[8, 3, 9, 4], X[2, 13, 3, 14],
X[12, 5, 13, 6], X[4, 9, 5, 10], X[16, 12, 1, 11], X[10, 16, 11, 15]]
|
In[4]:=
|
{GaussCode[K], GaussCode[L]}
|
Out[4]=
|
{GaussCode[1, -4, 3, -6, 5, -1, 2, -3, 6, -8, 7, -5, 4, -2, 8, -7],
GaussCode[{1, -7, 2, -8}, {-5, 4, -6, 3},
{7, -1, -4, 5, 8, -2, -3, 6}]}
|
In[5]:=
|
DTCode[K]
|
Out[5]=
|
DTCode[6, 8, 12, 14, 4, 16, 2, 10]
|
In[6]:=
|
br = BR[K]
|
Out[6]=
|
BR[3, {-1, -1, 2, -1, 2, -1, 2, 2}]
|
In[7]:=
|
Show[BraidPlot[br]]
|
|
|
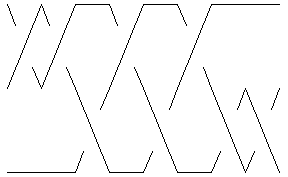
|
Out[7]=
|
-Graphics-
|
In[8]:=
|
{First[br], Crossings[br], BraidIndex[K]}
|
Out[8]=
|
{3, 8, 3}
|
In[9]:=
|
Show[DrawMorseLink[K]]
|
|
|
|
Out[9]=
|
-Graphics-
|
In[10]:=
|
Show[DrawMorseLink[L]]
|
|
|
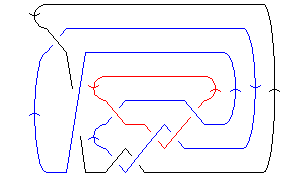
|
Out[10]=
|
-Graphics-
|
In[11]:=
|
(#[K]&) /@ {
SymmetryType, UnknottingNumber, ThreeGenus,
BridgeIndex, SuperBridgeIndex, NakanishiIndex
}
|
Out[11]=
|
{NegativeAmphicheiral, 1, 3, 3, 4, 1}
|
Polynomial Invariants
In[12]:=
|
alex = Alexander[K11][t]
|
Out[12]=
|
-4 5 12 20 2 3 4
-23 - t + -- - -- + -- + 20 t - 12 t + 5 t - t
3 2 t
t t
|
In[13]:=
|
Conway[K11][t]
|
Out[13]=
|
2 4 6 8
1 + t - 2 t - 3 t - t
|
"Similar" Knots (within the Atlas)
In[14]:=
|
Select[AllKnots[], (alex === Alexander[#][t])&]
|
Out[14]=
|
{Knot[11, Alternating, 57], Knot[11, Alternating, 108],
Knot[11, Alternating, 139], Knot[11, Alternating, 231]}
|
In[15]:=
|
{KnotDet[K], KnotSignature[K]}
|
Out[15]=
|
{37, 0}
|
In[16]:=
|
J=Jones[K11][q]
|
Out[16]=
|
-7 3 7 12 14 16 16 2 3 4
-12 + q - -- + -- - -- + -- - -- + -- + 10 q - 5 q + 2 q - q
6 5 4 3 2 q
q q q q q
|
"Similar" Knots (within the Atlas)
In[17]:=
|
Select[AllKnots[], (J === Jones[#][q] || (J /. q -> 1/q) === Jones[#][q])&]
|
Out[17]=
|
{Knot[11, Alternating, 57], Knot[11, Alternating, 231]}
|
In[18]:=
|
A2Invariant[K11][q]
|
Out[18]=
|
-20 -18 3 -14 -12 6 -6 3 4 2
5 + q - q + --- - q - q - -- + q - -- + -- + 2 q +
16 8 4 2
q q q q
4 6 8 10 12
4 q - 2 q - q - q - q
|
In[19]:=
|
HOMFLYPT[K11][a, z]
|
Out[19]=
|
2
4 2 4 2 4 z 2 2 4 2 4
12 - -- - 10 a + 3 a + 18 z - ---- - 19 a z + 6 a z + 10 z -
2 2
a a
4
z 2 4 4 4 6 2 6 4 6 2 8
-- - 15 a z + 4 a z + 2 z - 6 a z + a z - a z
2
a
|
In[20]:=
|
Kauffman[K11][a, z]
|
Out[20]=
|
4 2 4 4 z 11 z 3 5
12 + -- + 10 a + 3 a - --- - ---- - 17 a z - 16 a z - 6 a z -
2 3 a
a a
2 3 3
2 8 z 2 2 4 2 6 2 8 2 8 z 20 z
24 z - ---- - 22 a z - 2 a z + 3 a z - a z + ---- + ----- +
2 3 a
a a
4
3 3 3 5 3 7 3 4 11 z 2 4
29 a z + 35 a z + 16 a z - 2 a z + 28 z + ----- + 30 a z +
2
a
5 5
4 4 6 4 8 4 5 z 9 z 5 3 5
6 a z - 6 a z + a z - ---- - ---- - 14 a z - 29 a z -
3 a
a
6
5 5 7 5 6 8 z 2 6 4 6 6 6
16 a z + 3 a z - 21 z - ---- - 31 a z - 12 a z + 6 a z +
2
a
7 7 8
z 3 z 7 3 7 5 7 8 2 z 2 8
-- - ---- - 9 a z + 4 a z + 9 a z + 4 z + ---- + 10 a z +
3 a 2
a a
9
4 8 2 z 9 3 9 10 2 10
8 a z + ---- + 6 a z + 4 a z + z + a z
a
|